15.1 순환 뉴런과 순환 층
각 타임 스텝(time step, 또는 프레임)마다 순환 뉴런(recurrent neuron)은 $x_{(t)}$와 이전 타임 스텝의 출력인 $y_{(t-1)}$을 입력으로 받는다. 첫 번째 타임 스텝에서는 이전 출력이 없으므로 일반적으로 0으로 설정한다.
각 순환 뉴런은 두 벌의 가중치를 가진다. 하나는 입력 $x_{(t)}$를 위한 것이고 다른 하나는 이전 타임 스텝의 출력 $y_{(t-1)}$를 위한 것이다. 하나의 순환 뉴런이 아니라 순환 층 전체를 생각하면 가중치 벡터를 가중치 행렬 $W_{(x)}$와 $W_{(y)}$로 바꿀 수 있다. 순환 층 전체의 출력 벡터는 아래와 같이 계산된다.
$y_{(t)}=\phi (W_{(x)}^T x_{(t)} + W_{(y)}^T y_{(t-1)} + b)$
$b$: 편향
$\phi$: RELU와 같은 활성화 함수
피드포워드 신경망처럼 타임 스텝 t에서의 모든 입력을 행렬 $X_{(t)}$로 만들어 미니배치 전체에 대해 순환 층의 출력을 한 번에 계산할 수 있다.
$Y_{(t)} = \phi (X_{(t)} W_x + Y_{(t-1)} W_y + b)$
$= \phi ([X_{(t)} Y_{(t-1)}] W + b)$
$W = {W_x \choose W_y}$
$Y_{(t)}$: 타임 스텝 t에서 미니배치에 있는 각 샘플에 대한 층의 출력을 담은 $m \times n_{neurons}$ 행렬($m$은 미니배치에 있는 샘플 수, $n_{neurons}$는 뉴런 수)
$X_{(t)}$: 모든 샘플의 입력값을 담은 $m \times n_{inputs}$ 행렬($n_{inputs}$는 입력 특성 수)
$W_x$: 현재 타임 스텝의 입력에 대한 연결 가중치를 담은 $n_{inputs} \times n_{outputs}$ 행렬
$W_y$: 이전 타임 스텝의 출력에 대한 연결 가중치를 담은 $n_{nuerons} \times n_{nuerons}$ 행렬
$b$: 각 뉴런의 편향을 담은 $n_{neurons}$ 크기의 벡터
$Y_{(t)}$는 시간 $t=0$에서부터 모든 입력에 대한 함수가 된다.
15.1.2 입력과 출력 시퀀스
RNN은 입력 시퀀스를 받아 출력 시퀀스를 만들 수 있다. 이를 시퀀스-투-시퀀스 네트워크(sequence-to-sequence network)라 하며, 주식가격 같은 시계열 데이터를 예측하는 데 유용하다. 최근 N일치의 주식가격을 주입하면 네트워크는 각 입력값보다 하루 앞선 가격을 출력해야 한다.
또는 입력 시퀀스를 네트워크에 주입하고 마지막을 제외한 모든 출력을 무시할 수 있다. 이는 시퀀스-투-벡터 네트워크(sequence-to-vector network)로 영화 리뷰에 있는 연속된 단어를 주입하면 네트워크는 감성 점수를 출력한다.
반대로 각 타임 스텝에서 하나의 입력 벡터를 반복해서 네트워크에 주입하고, 하나의 시퀀스를 출력할 수 있다. 이는 벡터-투-시퀀스 네트워크(vector-to-sequence network)로 이미지(또는 CNN 출력)를 입력하여 이미지에 대한 캡션을 출력할 수 있다.
마지막으로 인코더(encoder)라 부르는 시퀀스-투-벡터 네트워크 뒤에 디코더(decoder)라 부르는 벡터-투-시퀀스 네트워크를 연결할 수 있다. 한 언어의 문장을 다른 언어로 번역하는 데 사용할 수 있다.
15.2 RNN 훈련하기
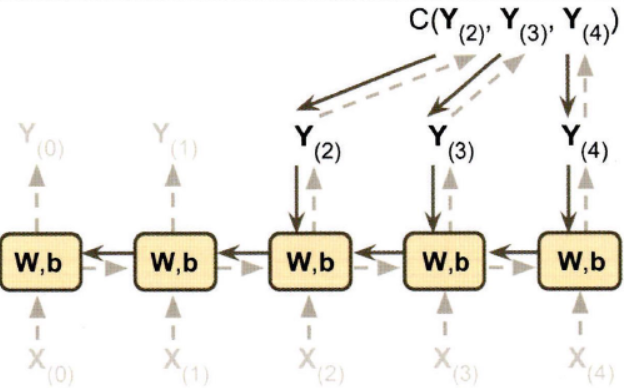
RNN을 훈련하기 위한 기법은 타임 스텝으로 네트워크를 펼치고 보통의 역전파를 사용하는 것인데, 이를 BPTT(backpropagation through time)라고 한다.
모델 파라미터는 BPTT 동안 계산된 그레이디언트를 사용하여 업데이트된다. 그레이디언트가 마지막 출력뿐만 아니라 비용 함수를 사용한 모든 출력에서 역방향으로 전파된다. 각 타임 스텝마다 같은 매개변수 $W$와 $b$가 사용되기 때문에 역전파가 진행되면 모든 타임 스텝에 걸쳐 합산될 것이다.
15.3 시계열 예측하기
웹사이트에서 시간당 접속 사용자 수, 도시의 날짜별 온도, 여러 지표를 사용한 기업의 분기별 재정 안정성 등을 연구한다고 가정해보자. 이런 경우 모두 데이터는 타임 스텝마다 하나 이상의 값을 가진 시퀀스며, 이를 시계열(time series)이라 부른다. 처음 두 예는 타임 스텝마다 하나의 값을 가지므로 단변량 시계열(univariate time series)이고, 재정 안정성 예시는 타임 스텝마다 여러 값(회사 수입 및 부채 등)이 있으므로 다변량 시계열(multivariate time series)이다.
def generate_time_series(batch_size, n_steps):
freq1, freq2, offsets1, offsets2 = np.random.rand(4, batch_size, 1)
time = np.linspace(0, 1, n_steps)
series = 0.5 * np.sin((time - offsets1) * (freq1 * 10 + 10)) # 웨이브 1
series += 0.2 * np.sin((time - offsets2) * (freq2 * 20 + 20)) # + 웨이브 2
series += 0.1 * (np.random.rand(batch_size, n_steps) - 0.5) # + 잡음
return series[..., np.newaxis].astype(np.float32) # [배치 크기, 타임 스텝 수, 1] 크기의 넘파이 배열 반환시계열을 다룰 때 입력 특성은 일반적으로 [배치 크기, 타임 스텝 수, 차원 수] 크기의 3D 배열로 나타난다.
np.random.seed(42)
n_steps = 50
series = generate_time_series(10000, n_steps + 1)
X_train, y_train = series[:7000, :n_steps], series[:7000, -1]
X_valid, y_valid = series[7000:9000, :n_steps], series[7000:9000, -1]
X_test, y_test = series[9000:, :n_steps], series[9000:, -1]15.3.1 기준 성능
RNN을 시작하기 전 기준 성능을 준비하는 가장 간단한 방법은 각 시계열의 마지막 값을 그대로 예측하는(naive forecasting) 것이다.
y_pred = X_valid[:, -1]
np.mean(keras.losses.mean_squared_error(y_valid, y_pred))또 다른 간단한 방법은 완전 연결 네트워크를 사용하는 것이다. 이 네트워크는 입력마다 1차원 특성 배열을 기대하기 때문에 Flatten 층을 추가해야 한다.
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[50, 1]),
keras.layers.Dense(1)
])15.3.2 간단한 RNN 구현하기
간단한 RNN은 아래와 같다.
model = keras.models.Sequential([
keras.layers.SimpleRNN(1, input_shape=[None, 1])
])순환 신경망은 어떤 길이의 타임 스텝도 처리할 수 있어 입력 시퀀스의 길이를 지정할 필요가 없다. 기본적으로 SimpleRNN 층은 하이퍼볼릭 탄젠트 활성화 함수를 사용한다.
기본적으로 케라스의 순환 층은 최종 출력만 반환한다. 타임 스텝마다 출력을 반환하려면 return_sequences=True 로 지정해야 한다.
트렌드와 계절성
시계열 예측 방법에는 가중 이동 평균(weighted moving average)이나 자동 회귀 누적 이동 평균(ARIMA, autoregressive integrated moving average) 등이 있다. 이런 방법 중 일부는 트렌드나 계절성을 제거해야 한다. RNN은 일반적으로 이런 작업이 모두 필요 없다.
15.3.3 심층 RNN
아래처럼 셀을 여러 층으로 쌓은 것을 심층 RNN(deep RNN)이라고 한다.
model = keras.models.Sequential([
keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None, 1]),
keras.layers.SimpleRNN(20, return_sequences=True),
keras.layers.SimpleRNN(1)
])마지막 층(=출력층)은 보통 은닉 상태가 필요하지 않아 Dense 층으로 바꾸는 경우가 많다. 따라서 마지막에서 두 번째 순환 층에서 return_sequences=True 를 제거해야 한다.
model = keras.models.Sequential([
keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None, 1]),
keras.layers.SimpleRNN(20),
keras.layers.Dense(1)
])이렇게 모델을 훈련하면 빠르게 수렴하고 성능도 좋다. 또 출력층의 활성화 함수를 원하는 함수로 바꿀 수 있다.
15.3.4 여러 타임 스텝 앞을 예측하기
타깃을 적절히 바꿔 여러 타임 스텝 앞의 값을 예측할 수 있다. 첫 번째 방법은 이미 훈련된 모델을 사용하여 다음 값을 예측한 다음 이 값을 입력으로 추가하는 것이다.
series = generate_time_series(1, n_steps + 10)
X_new, Y_new = series[:, :n_steps], series[:, n_steps]
X = X_new
for step_ahead in range(10):
y_pred_one = model.predict(X[:, step_ahead:])[:, np.newaxis, :]
X = np.concatenate([X, y_pred_one], axis=1)
Y_pred = X[:, n_steps:]두 번째 방법은 RNN을 훈련하여 다음 값 10개를 한 번에 예측하는 것이다.
series = generate_time_series(10000, n_steps + 10)
X_train, Y_train = series[:7000, :n_steps], series[:7000, -10:, 0]
X_valid, Y_valid = series[7000:9000, :n_steps], series[7000:9000, -10:, 0]
X_test, Y_test = series[9000:, :n_steps], series[9000:, -10:, 0]1개 유닛이 아닌 10개 유닛을 가진 출력층이 필요하다.
model = keras.models.Sequential([
keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None, 1]),
keras.layers.SimpleRNN(20),
keras.layers.Dense(10)
])
Y_pred = model.predict(X_new)위처럼 마지막 타임 스텝에서만 다음 값 10개를 예측하도록 모델을 훈련하는 대신 모든 타임 스텝에서 다음 값 10개를 예측하도록 모델을 훈련할 수 있다. 즉, 시퀀스-투-시퀀스 RNN으로 바꿀 수 있다. 이 방식의 장점은 모든 타임 스텝에서 RNN 출력에 대한 항이 손실에 포함된다는 것이다. 즉, 더 많은 오차 그레이디언트가 모델로 흐르고 시간에 따라서만 흐를 필요가 없어 훈련을 안정적으로 만들고 속도를 높일 수 있다.
Y = np.empty((10000, n_steps, 10)) # 타겟 역시 10차원의 시퀀스
for step_ahead in range(1, 10 + 1):
Y[:, :, step_ahead - 1] = series[:, step_ahead:step_ahead + n_steps, 0]
Y_train = Y[:7000]
Y_valid = Y[7000:9000]
Y_test = Y[9000:]다시 말해 타임 스텝 0에서 모델이 타임 스텝 1~10까지 예측하고, 타임 스텝 1에서 모델이 타임 스텝 2~11가지 예측하는 방식이다. 각 타깃은 입력 시퀀스와 동일한 길이의 시퀀스다.
위 모델을 시퀀스-투-시퀀스 모델로 바꾸려면 모든 순환 층에 return_sequences=True 를 지정하고, 모든 타임 스텝에서 출력을 Dense 층에 적용해야 한다. 케라스는 이를 위해 TimeDistributed 층을 제공한다. 이 층은 다른 층을 감싸 입력 시퀀스의 모든 타임 스텝에 이를 적용한다. 각 타임 스텝을 별개의 샘플처럼 다루도록 입력의 크기를 바꿔 이를 효과적으로 수행할 수 있다([배치 크기, 타임 스텝 수, 입력 차원] -> [배치 크기 x 타임 스텝 수, 입력 차원]). 그다음 Dense 층에 적용하고 출력 크기를 시퀀스로 되돌린다([배치 크기 x 타임 스텝 수, 출력 차원] -> [배치 크기, 타임 스텝 수, 출력 차원]).
model = keras.models.Sequential([
keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None, 1]),
keras.layers.SimpleRNN(20, return_sequences=True),
keras.layers.TimeDistributed(keras.layers.Dense(10))
])참고로 TimeDistributed 층을 도식으로 잘 설명한 아마추어 퀀트님의 블로그 내용이 있다. 위에서 말한 모든 타임 스텝에서 출력을 Dense 층에 적용하고 있고, 그 결과 각 스텝에서 역전파도 수행된다.
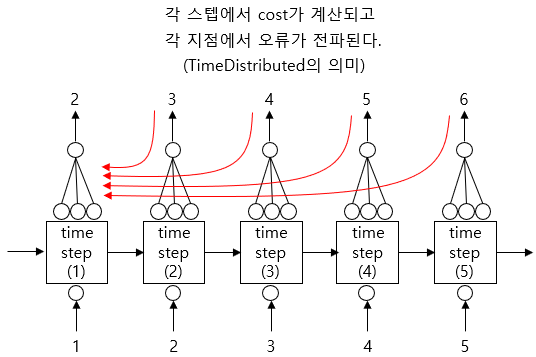
핸즈온 머신러닝 설명 중 위 빨간색 표시 부분의 의미가 헷갈릴 수 있다. TimeDistributed 층을 코드단에서 한 줄만 작성하면 그 위 RNN 층들을 감싸 모든 타임 스텝에 적용하게끔 하는 기능이 있다고 생각하면 된다.
https://keras.io/ko/layers/wrappers/
훈련하는 동안 모든 출력이 필요하지만 예측과 평가에는 마지막 타임 스텝의 출력만 사용된다.
def last_time_step_mse(Y_true, Y_pred):
return keras.metrics.mean_squared_error(Y_true[:, -1], Y_pred[:, -1])
optimizer = keras.optimizers.Adam(lr=0.01)
model.compile(loss='mse', optimizer=optimizer, metrics=[last_time_step_mse])15.4 긴 시퀀스 다루기
긴 시퀀스로 RNN을 훈련하면 많은 타임 스텝에 걸쳐 실행하므로 펼친 RNN이 매우 깊은 네트워크가 된다. 보통 심층 신경망처럼 그레이디언트 소실 및 폭주 문제가 발생할 수 있다.
15.4.1 불안정한 그레이디언트 문제와 싸우기
RNN에는 수렴하지 않는 활성화 함수보다 하이퍼볼릭 탄젠트 같은 수렴하는 활성화 함수가 적합하다. 또 하나, RNN에 잘 맞는 정규화는 배치 정규화가 아닌 층 정규화(layer normalization)이다. 배치 정규화와 비슷하지만 특성 차원에 대해 정규화한다는 것이 차이점이다.
한 가지 장점은 샘플에 독립적으로 타임 스텝마다 동적으로 필요한 통계를 계산할 수 있다는 것이다. 즉, 훈련 세트의 모든 샘플에 대한 특성 통계를 추정하기 위해 지수 이동 평균이 필요하지 않다. 배치 정규화와 마찬가지로 입력마다 하나의 스케일과 이동 파라미터를 학습한다. RNN에서 층 정규화는 일반적으로 입력과 은닉 상태의 선형 조합 직후에 사용된다.
class LNSimpleRNNCell(keras.layers.Layer):
def __init__(self, units, activation='tanh', **kwargs):
super().init__(**kwargs)
self.state_size = units
self.output_size = units
self.simple_rnn_cell = keras.layers.SimpleRNNCell(units, activation=None)
self.layer_norm = keras.layers.LayerNormalization()
self.activation = keras.activations.get(activation)
def call(self, inputs, states):
outputs, new_states = self.simple_rnn_cell(inputs, states)
norm_outputs = self.activation(self.layer_norm(outputs))
return norm_outputs, [norm_outputs]위 사용자 정의 셀을 사용하려면 keras.layers.RNN 층을 만들어 이 셀의 객체를 전달하면 된다.
model = keras.models.Sequential([
keras.layers.RNN(LNSimpleRNNCell(20), return_sequences=True,
input_shape=[None, 1]),
keras.layers.RNN(LNSimpleRNNCell(20), return_sequences=True),
keras.layers.TimeDistributed(keras.layers.Dense(10))
])15.4.2 단기 기억 문제 해결하기
LSTM 셀
장단기 메모리(LSTM, long short-term memory) 셀은 RNN의 매 훈련 스텝 후 사라지는 정보 문제를 해결하기 위해 고안된 기법이다.1
model = keras.models.Sequential([
keras.layers.LSTM(20, return_sequences=True, input_shape=[None, 1]),
keras.layers.LSTM(20, return_sequences=True),
keras.layers.TimeDistributed(keras.layers.Dense(10))
])아래는 LSTM 구조이다.
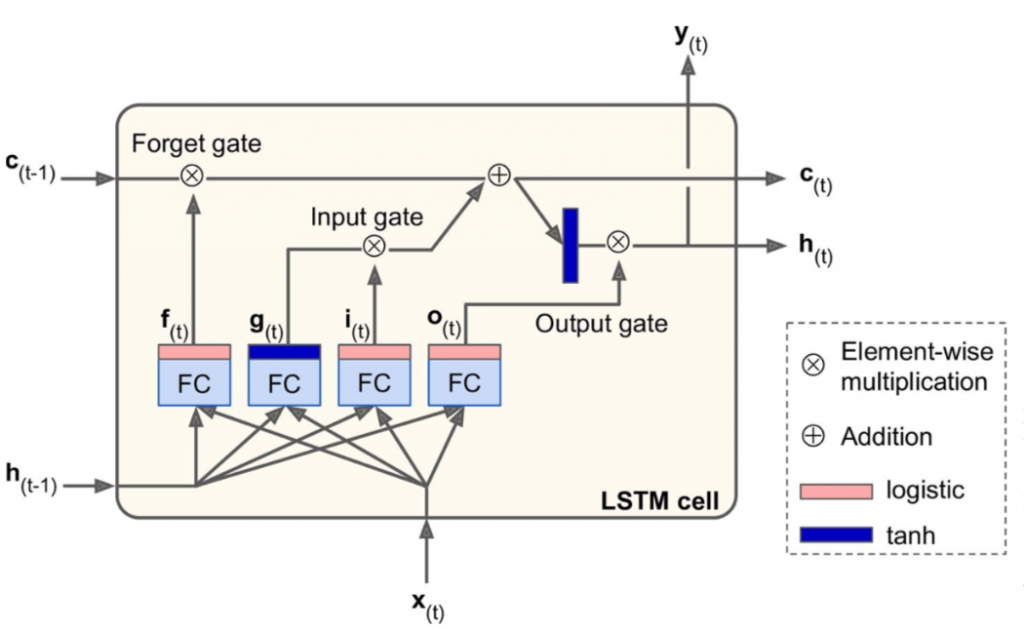
$h_{(t)}$: 단기 상태(short-term state)
$c_{(t)}$: 장기 상태(long-term state)
LSTM의 핵심 아이디어는 네트워크가 장기 상태에 저장할 것, 버릴 것, 그리고 읽어들일 것을 학습하는 것이다.
장기기억 $c_{(t-1)}$ 네트워크 통과 순서는
1. 삭제 게이트(forget gate)에서 일부 기억 소실
2. 입력 게이트(input gate)에서 선택한 기억 추가
3. 1) 다른 추가 변환 없이 바로 출력 <- $c_{(t)}$
2) 덧셈 연산 후 장기(long-term) 상태가 복사되어 tanh 함수로 전달 후 출력 게이트(output gate)에 의해 걸러짐 <- $h_{(t)}$
과 같다. 새로운 기억이 들어오는 곳과 게이트가 어떻게 작동되는지 살펴보자.
현재 입력 벡터 $x_{(t)}$와 이전 단기 상태 $h_{(t-1)}$이 네 개의 다른 완전 연결 층(FC)에 주입된다.
주 층은 $g_{(t)}$를 출력하는 층
ㄴ 현재 입력 $x_{(t)}$와 이전 단기 상태 $h_{(t-1)}$을 분석하는 일반적인 역할
ㄴ 장기 상태에 가장 중요한 부분이 저장
게이트 제어기(gate controller)
ㄴ 로지스틱 활성화 함수 사용(출력 범위 0 ~ 1)
ㄴ 원소별 곱셈 연산으로 주입되어 0을 출력하면 게이트를 닫고, 1을 출력하면 게이트를 여는 구조
1) 삭제 게이트($f_{(t)}$): 장기 상태의 어느 부분이 삭제되어야 하는지 제어
2) 입력 게이트($i_{(t)}$): $g_{(t)}$의 어느 부분이 장기 상태에 더해져야 하는지 제어
3) 출력 게이트($o_{(t)}$): 장기 상태의 어느 부분을 읽어서 현재 타임 스텝의 $h_{(t)}$와 $y_{(t)}$로 출력해야 하는지 제어
하나의 샘플에 대해 타임 스텝마다 행해지는 셀의 장기/단기 상태 및 출력 계산 수식은 아래와 같다.
$i_{(t)} = \sigma (W_{xi}^T x_{(i)} + W_{hi}^T h_{(t-1)} + b_i)$
$f_{(t)} = \sigma (W_{xf}^T x_{(i)} + W_{hf}^T h_{(t-1)} + b_f)$
$o_{(t)} = \sigma (W_{xo}^T x_{(i)} + W_{ho}^T h_{(t-1)} + b_o)$
$g_{(t)} = tanh(W_{xg}^T x_{(t)} + W_{hg}^T h_{(t-1)} + b_g)$
$c_{(t)} = f_{(t)} \otimes c_{(t-1)} + i_{(t)} \otimes g_{(t)}$
$y_{(t)} = h_{(t)} = o_{(t)} \otimes tanh(c_{(t)})$
텐서플로는 $b_f$를 0이 아닌 1로 채워진 벡터로 초기화해서 훈련 초기에 모든 것이 망각되는 것을 방지
GRU 셀
게이트 순환 유닛(GRU, gated recurrent unit) 셀은 2014년 조경현 등의 논문에서 제안됐다.2
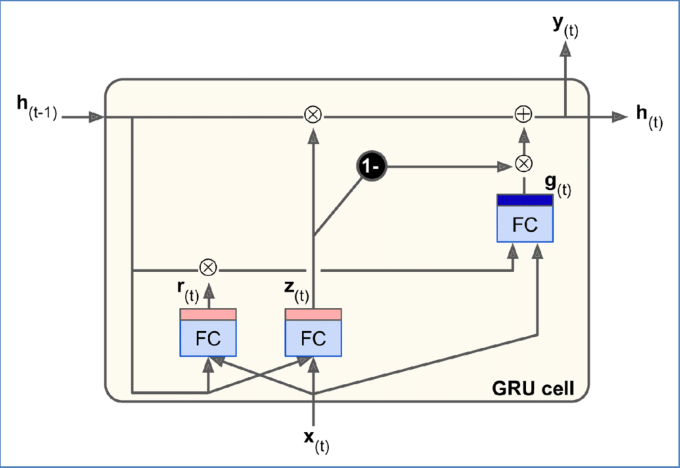
GRU 셀은 LSTM 셀의 간소화된 버전이고 작동 방식이 유사하다.
1. 두 상태 벡터(장기/단기)가 하나의 벡터 $h_{(t)}$로 합쳐짐
2. 하나의 게이트 제어기 $z_{(t)}$가 삭제 게이트 및 입력 게이트를 모두 제어
ㄴ 게이트 제어기가 1을 출력하면 삭제 게이트가 열리고(=1), 입력 게이트가 닫힘(1-1=0)
ㄴ 0을 출력하면 반대
ㄴ 기억이 저장될 때마다 저장될 위치가 먼저 삭제(흔한 LSTM 셀 변종)
3. 출력 게이트가 없음
ㄴ 전체 상태 벡터가 매 타임 스텝마다 출력
ㄴ 단, 이전 상태의 어느 부분이 주 층($g_{(t)}$)에 노출될지 제어하는 새로운 게이트 제어기 $r_{(t)}$ 존재
GRU 계산 방식은 아래와 같다.
$z_{(t)} = \sigma (W_{xz}^T x_{(t)} + W_{hz}^T h_{(t-1)} + b_z)$
$r_{(t)} = \sigma (W_{xr}^T x_{(t)} + W_{hr}^T h_{(t-1)} + b_r)$
$g_{(t)} = tanh(W_{xg}^T x_{(t)} + W_{hg}^T (r_{(t)} \otimes h_{(t-1)}) + b_g)$
$h_{(t)} = z{(t)} \otimes h_{(t-1)} + (1 - z_{(t)}) \otimes g_{(t)}$
LSTM과 GRU 셀은 단순한 RNN보다 훨씬 긴 시퀀스를 다룰 수 있지만 매우 제한적인 단기 기억을 가진다. 100 타임 스텝 이상의 시퀀스에서 장기 패턴을 학습하기 어렵다. 이를 해결하는 한 가지 방법은 1D 합성곱 층을 사용해 입력 시퀀스를 짧게 줄이는 것이다.
1D 합성곱 층을 사용해 시퀀스 처리하기
1D 합성곱 층의 몇 개의 커널들이 시퀀스 위를 슬라이딩하여 커널마다 1D 특성 맵을 출력한다. 각 커널은 매우 짧은 하나의 순차 패턴을 감지하도록 학습된다. 10개의 커널을 사용하면 이 층의 출력은 (모두 길이가 같은) 10개의 1차원 시퀀스로 구성된다. 스트라이드 1과 same 패딩으로 1D 합성곱 층을 사용하면 출력 시퀀스의 길이는 입력 시퀀스와 같다. 하지만 valid 패딩과 1보다 큰 스트라이드를 사용하면 출력 시퀀스는 입력 시퀀스보다 짧아진다.
아래 모델은 스트라이드 2를 사용해 입력 시퀀스를 두 배로 다운샘플링하는 1D 합성곱 층이다. 커널 크기를 스트라이드보다 크게 설정했기 때문에 모든 입력을 사용해 출력을 계산한다.
model = keras.models.Sequential([
keras.layers.Conv1D(filters=20, kernel_size=4, strides=2, padding='valid',
input_shape=[None, 1]),
keras.layers.GRU(20, return_sequences=True),
keras.layers.GRU(20, return_sequences=True),
keras.layers.TimeDistributed(keras.layers.Dense(10))
])
model.compile(loss='mse', optimizer='adam', metrics=[last_time_step_mse])
# kernel_size가 4이기 때문에 타깃 역시 4번째부터 시작
history = model.fit(X_train, Y_train[:, 3::2], epochs=20,
validation_data=(X_valid, Y_valid[:, 3::2])1D 합성곱 층에 대한 도식 설명은 딥러닝을 이용한 자연어 처리 입문에서 확인할 수 있다. 아래 그림을 보면 커널 크기는 3, valid 패딩을 사용하고 있고, 출력 시퀀스(길이: 7)가 입력 시퀀스(길이: 9)보다 짧다.
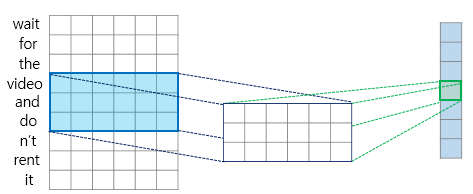
위처럼 설정하면 모델은 중요하지 않은 세부 사항은 버리고 유용한 정보는 보존하도록 학습한다. 합성곱 층으로 시퀀스 길이를 줄이면 GRU 층이 더 긴 패턴을 감지하는 데 도움이 된다.
WAVENET
2016년 소개된 WaveNet3에선 층마다 (각 뉴런의 입력이 떨어져 있는 간격인) 팽창 비율(dilation rate)을 2배로 늘리는 1D 합성곱 층을 쌓는다. 말이 애매한데 그림부터 살펴보자.
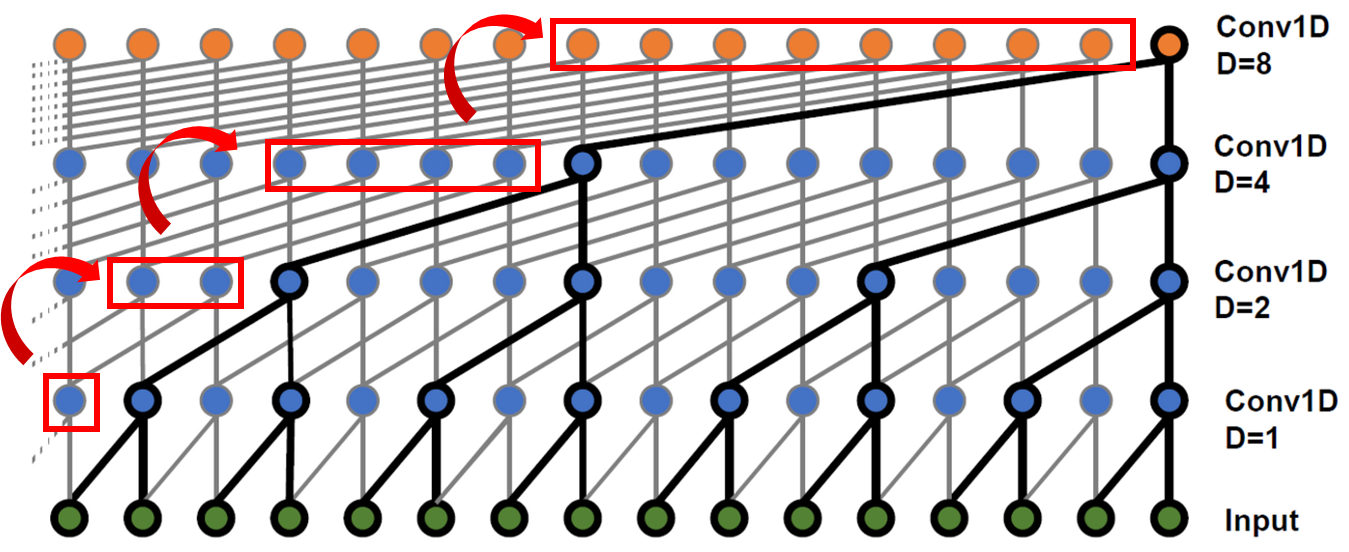
아래에서 위로 보지 말고 각 층에서 아래 뉴런들을 살펴보면 이해가 쉽다. 첫 번째 합성곱 층에서 2개의 타임 스텝(=입력층의 2개 뉴런)만 바라본다. 윗 층은 4개(=입력층의 4개 뉴런), 그 윗 층은 8개 타임 스텝을 본다. 이런 식으로 하위 층은 단기 패턴을 학습하고 상위 층은 장기 패턴을 학습한다. 팽창 비율을 2배 늘림으로써 아주 긴 시퀀스를 효율적으로 처리할 수 있는 것이다.
또한 각 층 이전의 팽창 비율과 동일한 개수의 0을 입력 시퀀스 왼쪽에 패딩으로 추가하여(그림 빨간색 박스 참고) 네트워크를 통과하는 시퀀스 길이를 동일하게 만들었다.
kernel_size가 2보다 큰 경우 dilation_rate * (kernel_size - 1)만큼 왼쪽에 0을 패딩으로 추가
이 패딩 방식을 사용하려면 padding='casual'로 지정
model = keras.models.Sequential()
model.add(keras.layers.InputLayer(input_shape=[None, 1]))
for rate in (1, 2, 4, 8) * 2:
model.add(keras.layers.Conv1D(filters=20, kernel_size=2, padding='casual',
activation='relu', dilation_rate=rate))
model.add(keras.layers.Conv1D(filters=10, kernel_size=1))
model.compile(loss='mse', optimizer='adam', metrics=[last_time_step_mse])
history = model.fit(X_train, Y_train, epochs=20,
validation_data=(X_valid, Y_valid))층에 추가한 패딩 덕분에 모든 합성곱 층은 입력 시퀀스의 길이와 동일한 시퀀스를 출력한다. 훈련하는 동안 전체 시퀀스를 타깃으로 사용하기 때문에 잘라내거나 다운샘플링할 필요가 없는 것이다.
'문돌이 존버 > 데이터 분석' 카테고리의 다른 글
| 핸즈온 머신러닝 2 복습하기(챕터 17: 오토인코더와 GAN을 사용한 표현 학습과 생성적 학습) (1) | 2024.01.05 |
|---|---|
| 핸즈온 머신러닝 2 복습하기(챕터 16: RNN과 어텐션을 사용한 자연어 처리) (2) | 2024.01.05 |
| 핸즈온 머신러닝 2 복습하기(챕터 14: 합성곱 신경망을 사용한 컴퓨터 비전) (0) | 2022.05.02 |
| 핸즈온 머신러닝 2 복습하기(챕터 11: 심층 신경망 훈련하기) (0) | 2022.01.01 |
| 버트(BERT) 개념 간단히 이해하기 (2) | 2021.11.17 |
