11.1 그레이디언트 소실과 폭주 문제
역전파 알고리즘은 출력층에서 입력층으로 오차 그레이디언트를 전파하면서 진행된다. 알고리즘이 신경망의 모든 파라미터에 대한 오차 함수의 그레이디언트를 계산하면 경사 하강법 단계에서 이 그레이디언트를 사용하여 각 파라미터를 수정한다.
하지만 알고리즘은 하위층으로 진행될수록 그레이디언트가 점점 작아지는 경우가 많다. 경사 하강법이 하위층의 연결 가중치를 변경하지 않은 채로 둔다면 훈련이 좋은 솔루션으로 수렴되지 않으며, 이 문제를 그레이디언트 소실(vanishing gradient)이라고 한다.
2010년 세이비어 글로럿(Xavier Glorot)과 요슈아 벤지오(Yoshua Bengio)가 발표한 논문1으로 인해 심층 신경망을 훈련할 때 그레이디언트를 불안정하게 하는 원인이 무엇인지 파악되었다. 여러 원인이 발견되었는데, 그중 하나는 로지스틱 시그모이드 활성화 함수와 그 당시 가장 인기 있던 가중치 초기화 방법(평균 0, 표준편차 1인 정규분포) 조합이었다.
신경망 위쪽으로 갈수록 층을 지날 때마다 분산이 계속 커져 가장 높은 층의 활성화 함수는 0이나 1로 수렴한다. 특히 로지스틱 함수의 평균이 0이 아니고 0.5라는 사실 때문에 더 나빠진다.(로지스틱 함수는 항상 양수를 출력하므로 출력의 가중치 합이 입력보다 커질 가능성이 높음)

11.1.1 글로럿과 He 초기화
예측을 할 때는 정방향으로, 역전파할 때는 그레이디언트를 역방향으로 하여 양방향 신호가 적절하게 흘러야 한다. 이를 위해 논문에선 각 층의 출력에 대한 분산이 입력에 대한 분산과 같아야 한다고 주장한다. 그리고 역방향에서 층을 통과하기 전과 후의 그레이디언트 분산이 동일해야 한다.
층의 입력과 출력 연결 개수(각각 fan-in, fan-out이라고 부름)가 같지 않으면 위의 2가지를 보장할 수 없다. 하지만 논문 저자들은 실전에서 매우 잘 작동한다고 입증된 대안을 제안했는데, 각 층의 연결 가중치를 아래와 같이 무작위로 초기화하는 것이다.
μ=0,σ=1fanavg인 정규분포
또는 r=√3fanavg일 때 −r과 +r 사이의 균등분포
fanavg=(fanin+fanout)/2
해당 초기화 전략을 저자 이름을 따서 세이비어 초기화 또는 글로럿 초기화라고 부른다. 글로럿 초기화를 사용하면 훈련 속도를 상당히 높일 수 있으며, 현재 딥러닝의 성공을 견인한 기술 중 하나이다.
세이비어 초기화는 S자 형태의 활성화 함수(시그모이드, 하이퍼볼릭탄젠트 등)와 함께 사용할 경우 좋은 성능을 보이지만, ReLU와 함께 사용할 때는 좋지 않다. ReLU는 아래에서 이야기할 He 초기화와 함께 사용하는 것이 좋다.
일부 논문들이 다른 활성화 함수에 대해 비슷한 전략을 제안했다. ReLU 활성화 함수에 대한 초기화 전략은 He 초기화, SELU 활성화 함수에 대한 초기화는 르쿤(LuCun) 초기화를 사용한다.
He 초기화: 2fanin
르쿤 초기화: 1fanin
예를 들어, He 초기화의 경우 정규 분포로 초기화하면 표준 편차가 다음을 만족하도록 한다.
σ=√2fanin
케라스는 기본적으로 균등분포의 글로럿 초기화를 사용한다. 하지만 다음과 같이 각 경우에 맞춰 다른 초기화를 지정할 수 있다.
keras.layers.Dense(10, activation='relu', kernel_initializer='he_normal') # he_uniformfanin 대신 fanout 기반의 균등분포 He 초기화를 사용할 경우 아래처럼 VarianceScaling 을 사용할 수 있다.
he_avg_init = keras.initializers.VarianceScaling(scale=2, mode='fan_avg', distribution='uniform')
keras.layers.Dense(10, activation='sigmoid', kernel_initializer=he_avg_init)
# VarianceScaling 클래스의 매개변수 기본값
VarianceScaling(scale=1, mode='fan_in', distribution='truncated_normal')
# kernel_initializer 매개변수 기본값 -> glorot_uniform
keras.initializers.VarianceScaling(scale=1, mode='fan_avg', distribution='uniform')
# he_normal일 경우
keras.initializers.VarianceScaling(scale=2, mode='fan_in', distribution='truncated_normal')truncated_normal의 경우, σ2=1.3×scale/mode로 계산
untruncated_normal의 경우, σ2=scale/mode로 계산
11.1.2 수렴하지 않는 활성화 함수
논문에서 얻은 통찰 중 하나는 활성화 함수를 잘못 선택하면 그레이디언트의 소실이나 폭주로 이어질 수 있다는 것이다. 생물학적 뉴런의 방식과 비슷한 시그모이드 활성화 함수가 최선의 선택이 아니라 다른 활성화 함수가 심층 신경망에서 훨씬 더 잘 작동했다.
ReLU 함수는 특정 양숫값에 수렴하지 않고 계산이 빠르다는 큰 장점이 있다. 하지만 죽은 ReLU(dying ReLU)로 알려진 문제가 있는데, 훈련하는 동안 일부 뉴런이 0 이외의 값을 출력하지 않는 것이다. 뉴런의 가중치가 바뀌면서 훈련 세트에 있는 모든 샘플에 대해 입력의 가중치 합이 음수가 되면 ReLU 함수의 그레이디언트가 0이 되어 경사 하강법이 더는 작동하지 않는다.
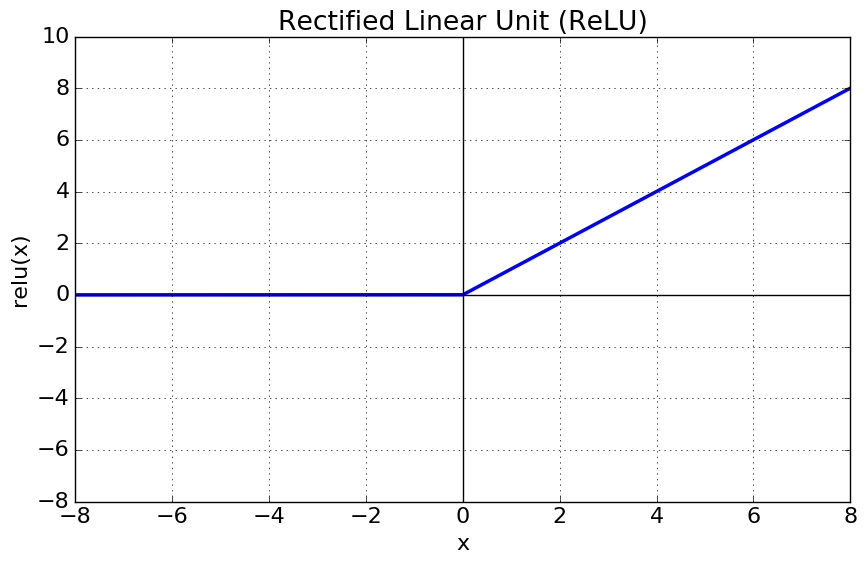
이를 해결하기 위해 LeakyReLU 같은 ReLU 함수의 변종을 사용한다. 이 함수는 LeakyReLUα(z)=max(αz,z)로 정의된다. 하이퍼파라미터 α가 이 함수가 "새는(leaky)" 정도를 결정한다. 새는 정도란 z<0일 때 이 함수의 기울기를 가리키며, 일반적으로 0.01로 설정한다.
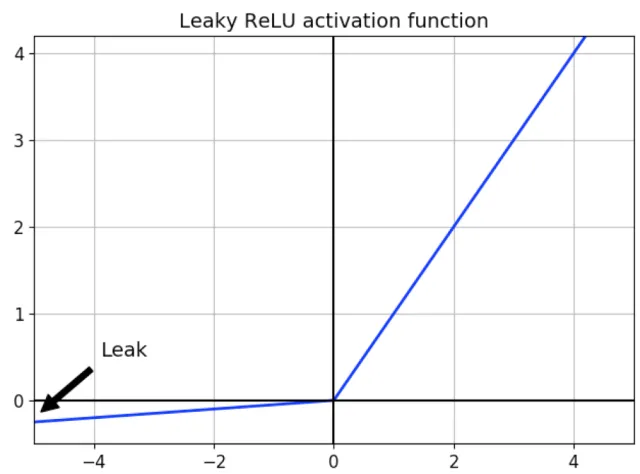
또 다른 변종인 RReLU(randomized leaky ReLU)와 PReLU(parametric leaky ReLU)도 있다. RReLU는 훈련하는 동안 주어진 범위에서 α를 무작위로 선택하고 테스트시에는 평균을 사용하는 것이다. PReLU는 α가 훈련하는 동안 학습되는 것으로, 하이퍼파라미터가 아니라 역전파에 의해 변경되는 파라미터다.
툐르크-아르네 클레브르트(Djork-Ame Clevert) 등의 2015년 논문2은 ELU(exponential linear unit)라는 새로운 활성화 함수를 제안했다. 훈련 시간이 줄고 신경망의 테스트 세트 성능도 높아 다른 모든 ReLU 변종의 성능을 앞질렀다.
ELUα(z)=α(exp(z)−1), z<0일때
z, z≥0일때
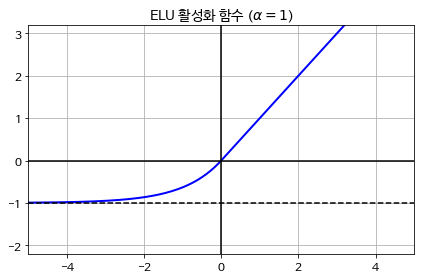
α: z가 큰 음숫값일 때 ELU가 수렴할 값을 정의하며, 보통 1로 설정
α=1이면 이 함수는 z=0에서 급격히 변동하지 않으므로 z=0을 포함해 모든 구간에서 매끄러워 경사 하강법의 속도를 높임
ELU 활성화 함수의 단점은 지수 함수를 사용하므로 계산이 느리다는 것이다. 앞에서 훈련 시간이 줄었다고 한 것은 수렴 속도가 빠르다는 것임에 주의하자.
권터 클람바우어(Gunter Klambauer) 등의 2017년 논문3은 SELU(Scaled ELU) 활성화 함수를 소개했다. 완전 연결 층만 쌓아서 신경망을 만들고 모든 은닉층이 SELU 활성화 함수를 사용하면 네트워크가 자기 정규화(self-normalize)된다고 한다. 즉 훈련하는 동안 각 층의 출력이 평균 0과 표준편차 1을 유지하는 경향이 있다는 것이다.
하지만 자기 정규화가 일어나기 위한 몇 가지 조건이 있다.
1. 입력 특성이 반드시 표준화(평균 0, 표준편차 1)되어야 한다.
2. 모든 은닉층의 가중치는 르쿤 정규분포 초기화로 초기화되어야 한다. 케라스에서는 kernal_initializer='lecun_normal'로 설정한다.
3. 네트워크는 일렬로 쌓은 층으로 구성되어야 한다.
LeakyReLU 활성화 함수를 사용하려면 LeakyReLU 층을 만들고 모델에서 적용하려는 층 뒤에 추가하면 된다.
model = keras.models.Sequential([
...
keras.layers.Dense(10, kernel_initializer='he_normal'),
keras.layers.LeakyReLU(alpha=0.2),
...
])SELU 활성화 함수를 사용하려면 아래와 같이 지정한다.
layer = keras.layers.Dense(10, activation='selu', kernel_initializer='lecun_normal')11.1.3 배치 정규화
ELU(혹은 다른 ReLU 변종)와 함께 He 초기화를 사용하면 훈련 초기 단계에서 그레이디언트 소실이나 폭주 문제를 크게 감소할 수 있다. 하지만 훈련하는 동안 다시 발생하지 않으리란 보장은 없다. 일례로 신경망 내부 각 층을 통과할 때마다 입력 데이터의 분포가 조금씩 변경되는 현상이 발생할 수 있다. 이것이 Internal Covariate Shift라고 불리는 문제다.
2015년 세르게이 이오페(Sergey Ioffe)와 치리슈티언 세게지(Christian Szegedy)가 이를 해결하기 위한 배치 정규화(Batch Normalization, 이하 BN) 기법을 제안했다. 각 층에서 활성화 함수를 통과하기 전이나 후에 모델에 연산을 하나 추가하는 것이다(CNN에선 보통 Conv 이후, 활성화 함수 이전에 적용). 단순하게 입력을 원점에 맞추고 정규화한 다음, 각 층에서 2개의 새로운 파라미터로 결괏값의 스케일을 조정하고 이동시킨다.
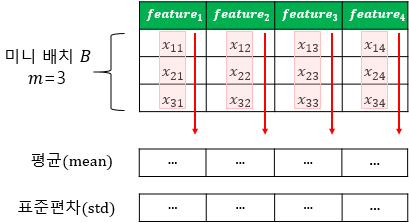
BN 알고리즘은 아래와 같으며, 현재 미니배치에서 입력의 평균과 표준편차를 평가한다.
1. μB=1mB∑mBi=1x(i)
2. σ2B=1mB∑mBi=1(x(i)−μB)2
3. ˆx(i)=x(i)−μB√σ2B + ε
4. z(i)=γ⊗ˆx(i)+β
μB: 미니배치 B에 대해 평가한 입력의 평균 벡터
σB: 미니배치에 대한 평가한 입력의 표준편차 벡터
μB: 미니배치에 있는 샘플 수
ˆx(i): 평균이 0이고 정규화된 샘플 i의 입력
γ: 층의 출력 스케일 파라미터 벡터(표준편차와 비슷한 개념)
⊗: 원소별 곱셈(element-wise multiplication)
β: 층의 출력 이동 파라미터 벡터(평균 이동)
ε: 분모가 0이 되는 것을 막기 위한 작은 숫자(보통 10−5), 안전을 위한 항(smoothing term)이라 부름
z(i): 배치 정규화 연산의 출력, 즉 입력 스케일을 조정하고 이동시킨 결과
훈련하는 동안 배치 정규화는 입력을 정규화한 다음 스케일을 조정하고 이동시킨다. 하지만 테스트 시에는 샘플의 배치가 아니라 샘플 하나에 대한 예측을 만들어야 하는데, 이 경우 입력의 평균과 표준편차를 계산할 방법이 없다. 한 가지 방법은 훈련이 끝난 후 전체 훈련 세트를 신경망에 통과시켜 배치 정규화층의 각 입력에 대한 평균과 표준편차를 계산하는 것이다.
하지만 대부분 배치 정규화 구현은 층의 입력 평균과 표준편차의 지수 가중 이동 평균(exponentially weighted average)을 사용해 훈련하는 동안 최종 통계를 추정한다. 케라스의 BatchNormalization 층은 이를 자동으로 수행한다.
정리하면 배치 정규화 층마다 4개의 파라미터가 학습된다. γ(출력 스케일 벡터)와 β(출력 이동 벡터)는 일반적인 역전파를 통해 학습된다. μ(최종 입력 평균 벡터)와 σ(최종 입력 표준편차 벡터)는 지수 가중 이동 평균을 사용하여 추정된다. μ와 σ는 훈련하는 동안 추정되지만 훈련이 끝난 후 사용된다.
배치 정규화는 모델의 복잡도를 키우며 층마다 추가되는 계산으로 신경망의 예측을 느리게 한다. 하지만 수렴이 훨씬 빨라지므로 보통 상쇄되기 때문에 더 적은 에포크로 동일한 성능에 도달할 수 있다.
배치 정규화는 전체 데이터셋이 아니라 미니배치마다 평균과 표준편차를 계산하므로 훈련 데이터에 일종의 잡음(noise)을 넣는다고 볼 수 있다. 하지만 배치 정규화로 인한 규제(regularization)는 부수 효과여서 규제를 위해선 드롭아웃(dropout)을 함께 사용하는 것이 좋다.
# 활성화 함수 이후 배치 정규화 층 추가
model = keras.Model.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.BatchNormalization(),
keras.layers.Dense(300, activation='elu', kernel_initializer='he_normal'),
keras.layers.BatchNormalization(),
keras.layers.Dense(100, activation='elu', kernel_initializer='he_normal'),
keras.layers.BatchNormalization(),
keras.layers.Dense(10, activation='softmax')
])model.summary()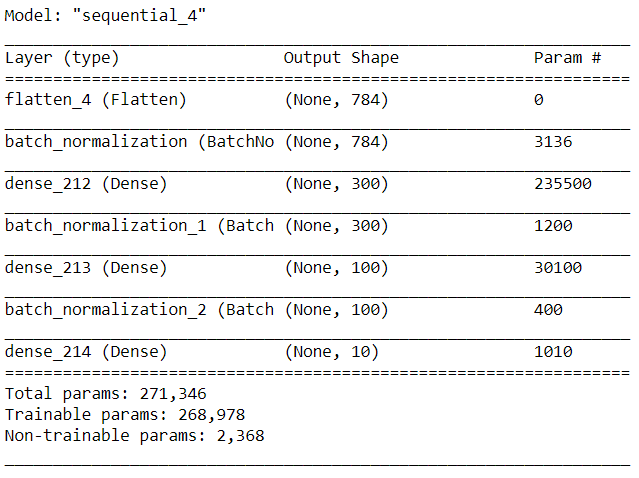
위 결과에서 알 수 있듯 배치 정규화 층은 입력마다 4개의 파라미터 γ,β,μ,σ를 추가한다(1번 배치 정규화 층 파라미터 개수: 4 x 784 = 3,136). 마지막 2개 파라미터 μ,σ는 이동 평균으로 역전파로 학습되지 않기 때문에 케라스는 'Non-trainable'로 분류한다(2,368 = (3,136 + 1,200 + 400) / 2)
[(var.name, var.trainable) for var in model.layers[1].variables]
케라스에서 배치 정규화 층을 만들 때, 훈련하는 동안 매 반복마다 케라스에서 호출될 2개의 연산이 함께 생성된다. 이 연산이 이동 평균을 업데이트한다.
배치 정규화 논문 저자들은 활성화 함수 이후보다 이전에 배치 정규화 층을 추가하는 것이 좋다고 한다. 하지만 선호되는 방식이 달라 2가지 방법 모두 실험해보고 확인할 필요가 있다. 활성화 함수 전에 배치 정규화 층을 추가하려면 은닉층에 활성화 함수를 지정하지 말고 배치 정규화 층 뒤에 별도의 층으로 추가해야 한다. 또한 배치 정규화 층은 입력마다 이동 파라미터를 포함하므로 이전 층에서 편향을 뺄 수 있다.
# 활성화 함수 이전 배치 정규화 층 추가
model = kears.Model.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.BatchNormalization(),
keras.layers.Dense(300, kernel_initializer='he_normal', use_bias=False), # 편향 포함 X
keras.layers.BatchNormalization(),
keras.layers.Activation('elu')
keras.layers.Dense(100, kernel_initializer='he_normal', use_bias=False),
keras.layers.BatchNormalization(),
keras.layers.Activation('elu'),
keras.layers.Dense(10, activation='softmax')
])BatchNormalization 클래스는 조정할 하이퍼파라미터가 적고 보통 기본값이 잘 작동하지만 가끔 momentum 매개변수를 변경해야 할 수도 있다. 지수 이동 평균을 업데이트할 때 해당 파라미터를 사용하며 아래 식으로 정의된다.
ˆv←ˆv×momentum+v×(1−momentum)
적절한 모멘텀 값은 일반적으로 1에 가까우며, 데이터셋이 크고 미니배치가 작으면 소수점 뒤에 9를 더 넣어 1에 가깝게 한다(예: 0.9, 0.99, 0.999).
위에서 언급한 것처럼 배치 정규화 층은 훈련 도중과 훈련이 끝난 후에 수행하는 계산이 다르다. 훈련하는 동안 배치 통계를 사용하고 훈련이 끝난 후에는 "최종" 통계(이동 평균의 마지막 값)를 사용한다. BN은 심층 신경망에서 매우 널리 사용하는 층이 되었고, 보통 모든 층 뒤에 배치 정규화가 있다고 가정한다. 하지만 훙이 장(Hongyi Zhang) 등의 최근 논문4에 따르면 배치 정규화 없이도 심층 신경망을 훈련해 이미지 분류 작업에서 최고 성능을 달성했기 때문에 해당 가정은 바뀔 수 있다.
(참고)
배치 정규화는 RNN에 적용하기 어렵다는 단점이 있기 때문에 층 정규화(Layer Normalization)를 사용하는 것이 좋을 때가 있다.

11.1.4 그레이디언트 클리핑
그레이디언트 폭주 문제를 완화하는 한 가지 방법은 역전파될 때 일정 임곗값을 넘어서지 못하게 그레이디언트를 잘라내는 것이다. 이를 그레이디언트 클리핑(gradient clipping)이라 하며 배치 정규화를 적용하기 어려운 순환 신경망에서 많이 사용한다.
케라스에선 옵티마이저를 만들 때 clipvalue 와 clipnorm 매개변수를 지정하면 된다.
optimizer = keras.optimizers.SGD(clipvalue=1.0)
model.comiple(loss='mse', optimizer=optimizer)위 옵티마이저는 그레이디언트 벡터의 모든 원소를 -1.0과 1.0 사이로 클리핑한다. 다시 말해 훈련되는 각 파라미터에 대한 손실의 모든 편미분 값을 -1.0에서 1.0으로 잘라내는 것이다. 예를 들어 원본 그레이디언트 벡터가 [0.9, 100.0]라면 대부분 2번째 축 방향을 향한다. 이를 클리핑하면 [0.9, 1.0]이 되고 거의 두 축 사이 대각선 방향을 향한다.
그레이디언트 벡터 방향을 바꾸지 못하게 하려면 clipvalue 대신 clipnorm 을 지정하여 노름으로 클리핑해야 한다. 만약 l2 노름이 지정한 임곗값보다 크면 전체 그레이디언트를 클리핑한다. clipnorm=1.0으로 지정하면 [0.00899964, 0.9999595]로 클리핑되므로 방향을 그대로 유지한다.
11.2 사전훈련된 층 재사용하기
일반적으로 아주 큰 규모의 DNN을 처음부터 새로 훈련하지 않는다. 해결하려는 것과 비슷한 유형의 문제를 처리한 신경망이 이미 있는지 찾아본 다음, 그 신경망의 하위층을 재사용하는 것이 좋은데 이를 전이 학습(transfer learning)이라 한다.
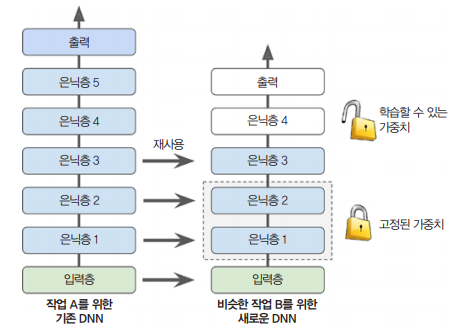
전이학습은 훈련 속도를 크게 높일 뿐만 아니라 필요한 훈련 데이터도 크게 줄여준다. 참고로 작업이 비슷할수록(낮은 층부터 시작해서) 더 많은 층을 재사용하는 것이 좋다.
11.2.1 케라스를 사용한 전이 학습
8개 클래스만 담겨 있는 패션 MNIST 데이터셋이 있다고 가정하자. 모델 A는 8개 클래스 모두를 분류하는 것이고, 모델 B는 샌들과 셔츠만 분류하는 이진 분류기다. 모델 B는 모델 A와 매우 비슷하여 전이 학습을 진행해보려고 한다.
model_A = keras.models.load_model('my_model_A.h5')
model_B_on_A = keras.models.Sequential(model_A.layers[:-1]) # 출력층 제외 모든 층 재사용
model_B_on_A.add(keras.layers.Dense(1, activation='sigmoid'))model_A와 model_B_on_A는 일부 층을 공유하기 때문에 model_B_on_A를 훈련할 때 model_A도 영향을 받는다. 이를 원치 않으면 층을 재사용하기 전에 model_A를 클론(clone)하면 된다.
model_A_clone = keras.models.clone_model(model_A)
model_A_clone.set_weights(model_A.get_weights())model_B_on_A를 훈련하면 새로운 출력층이 랜덤하게 초기화되어 있기 때문에 큰 오차를 만들고(적어도 처음 몇 번의 에포크 동안), 이는 곧 재사용된 가중치를 망칠 수 있다. 이를 해결하는 한 가지 방법은 처음 몇 번의 에포크 동안 재사용된 층을 동결(경사 하강법으로 가중치가 바뀌지 않도록 훈련되지 않는 가중치로 만드는 것)하고 새로운 층에 적절한 가중치를 학습할 시간을 주는 것이다.
for layer in model_B_on_A.layers[:-1]:
layer.trainable = False # 동결
# 층을 동결하거나 해제한 후에는 반드시 모델 컴파일을 해야 함
# compile() 메서드가 모델에서 훈련될 가중치를 모으기 때문
model_B_on_A.compile(loss='binary_crossentropy', optimizer='sgd', metrics=['accuracy'])그다음 재사용된 층의 동결을 해제하고 작업 B에 맞게 재사용된 층을 세밀하게 튜닝해야 한다. 일반적으로 재사용된 층의 동결을 해제한 후에 학습률을 낮추는 것이 재사용된 가중치가 망가지는 것을 막아준다.
history = model_B_on_A.fit(X_train_B, y_train_B, epochs=4,
validation_data=(X_valid_B, y_valid_B))
for layer in model_B_on_A.layers[:-1]:
layer.trainable = True # 동결 해제
optimizer = keras.optimizer.SGD(lr=1e-4) # 디폴트는 1e-2
model_B_on_A.compile(loss='binary_crossentropy', optimizer=optimizer, metrics=['accuracy'])
history = model_B_on_A.fit(X_train_B, y_train_B, epochs=16,
validation_data=(X_valid_B, y_valid_B))model_B_on_A.evaluate(X_test_B, y_test_B)
11.3 고속 옵티마이저
훈련 속도를 크게 높일 수 있는 또 다른 방법으로 표준적인 경사 하강법 옵티마이저 대신 더 빠른 옵티마이저가 있다.
1. 모멘텀 최적화(Momentum optimization)
2. 네스테로프 가속 경사(Nesterov accelerated gradient)
3. AdaGrad
4. RMSProp
5. Adam
6. Nadam
11.3.1 모멘텀 최적화
모멘텀 최적화의 원리는 다음과 같이 간단하다. 볼링공이 매끈한 표면의 완만한 경사를 따라 구를 때 처음에는 느리게 출발하지만 종단속도(terminal velocity)5에 도달할 때까지는 빠르게 가속될 것이다.
모멘텀 최적화는 표준 경사 하강법과 달리 이전 그레이디언트가 얼마였는지를 상당히 중요하게 생각한다. 매 반복에서 현재 그레이디언트를 (학습률 η를 곱한 후) 모멘텀 벡터 m에 더하고 이 값을 빼는 방식으로 가중치를 업데이트한다. 즉 그레이디언트를 속도가 아니라 가속도로 사용하는 것이다. 일종의 마찰저항을 표현하고 모멘텀이 너무 커지는 것을 막기 위해 이 알고리즘에는 모멘텀이라는 새로운 하이퍼파라미터 β가 있다. 해당 값은 0(높은 마찰저항) ~ 1(마찰저항 없음) 사이로 설정되며 보통 0.9이다.
1. m<βm−ηdθJ(θ)
2. θ<θ+m
dθJ(θ): 음수
m: 음수
위에서 모멘텀 벡터 m에 더하고 이 값을 빼는 방식으로 가중치를 갱신한다는 의미가 헷갈릴 수 있는데, 부호를 생각하면 1번 식은 결국 더하는 것이고, 2번 식은 결국 빼는 것을 의미
그레이디언트가 일정하다면 종단속도(=가중치를 업데이트하는 최대 크기)는 학습률 η를 곱한 그레이디언트에 (부호는 무시) 11−β를 곱한 것과 같음을 확인할 수 있다.6
케라스에서 모멘텀 최적화를 구현하는 명령어는 아래와 같다. 모멘텀 최적화는 최적점에 빠르게 도달하게 하고 지역 최적점을 건너뛰도록 도움을 준다.
optimizer = keras.optimizers.SGD(lr=0.001, momentum=0.9)11.3.2 네스테로프 가속 경사
1983년 유리 네스테로프(Yuri Nesterov)가 제안한 방법은 기본 모멘텀 최적화보다 거의 항상 빠르다. 네스테로프 가속 경사(이하 NAG)는 현재 위치가 θ가 아니라 모멘텀의 방향으로 조금 앞선 θ+βm에서 비용 함수의 그레이디언트를 계산하는 것이다.
1. m<βm−ηdθJ(θ+βm)
2. θ<θ+m
일반적으로 모멘텀 벡터가 올바른 방향(=최적점을 향하는 방향)을 가리킬 것이므로 NAG가 좀 더 효율적이다. 구현은 아래와 같이 쉽게 수행할 수 있다.
optimizer = keras.optimizers.SGD(lr=0.001, momentum=0.9, nesterov=True)11.3.3 AdaGrad
AdaGrad 알고리즘은 가장 가파른 차원을 따라 그레이디언트 벡터의 스케일을 감소시킨다.
1. s<s+dθJ(θ)⊗dθJ(θ)
2. θ<θ−ηdθJ(θ)⊘√s+ϵ
⊘: 원소별 나눗셈
ϵ: 일반적으로 10−10
첫 번째 단계는 그레이디언트의 제곱을 벡터 s에 누적하는 것이다. 두 번째 단계는 경사 하강법과 동일하지만 한 가지 차이는 그레이디언트 벡터를 √s+ϵ으로 나누어 스케일을 조정하는 것이다.
해당 알고리즘은 학습률을 감소시키지만 경사가 완만한 차원보다 가파른 차원에 대해 더 빠르게 감소된다. 이를 적응적 학습률(adaptive learning rate)이라 부르며, 전역 최적점 방향으로 더 곧장 가도록 업데이트하는 데 도움이 된다.
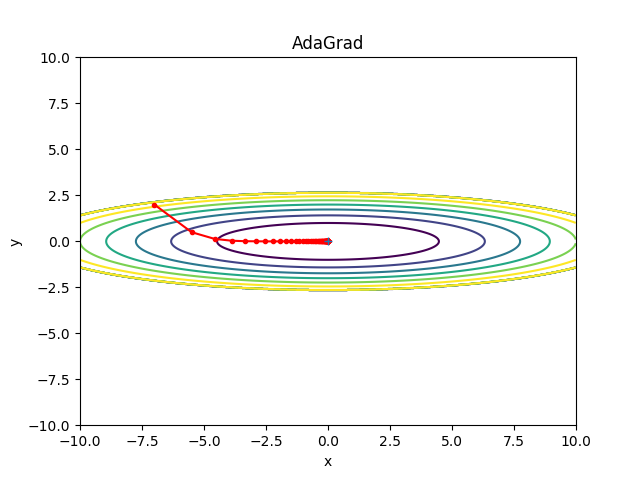
수식을 보면 그레이디언트 제곱값이 계속 누적되므로 시간이 지날수록 분모가 커짐을 알 수 있다. 다시 말하면 처음에는 큰 학습률이 적용되지만 최저점에 가까울수록 학습률이 작아지는 것이다. 다만, 학습률이 너무 감소되어 전역 최적점에 도착하기 전에 알고리즘이 완전히 멈춘다는 단점이 있다. 따라서 보통 복잡한 심층 신경망에는 사용하지 않는다.
11.3.4 RMSProp
RMSProp 알고리즘은 (훈련 시작부터의 모든 그레이디언트가 아닌) 가장 최근 반복에서 비롯된 그레이디언트만 누적함으로써 AdaGrad의 단점을 극복했다. 이를 위해 첫 번째 단계에서 지수 감소를 사용한다.
1. s<βs+(1−β)dθJ(θ)⊗dθJ(θ)
2. θ<θ−ηdθJ(θ)⊘√s+ϵ
보통 감쇠율 β는 0.9로 설정하지만 기본값이 잘 작동하므로 튜닝할 필요는 전혀 없다.
optimizer = keras.optimizers.RMSProp(lr=0.001, rho=0.9)11.3.5 Adam과 Nadam 최적화
적응적 모멘트 추정(adaptive moment estimation)을 의미하는 Adam은 모멘텀 최적화와 RMSProp의 아이디어를 합친 것이다. 모멘텀 최적화처럼 지난 그레이디언트의 지수 감소 평균(exponential decaying average)을 따르고 RMSProp처럼 지난 그레이디언트 제곱의 지수 감소된 평균을 따른다.
1. m<β1m−(1−β1)dθJ(θ)
2. s<β2s+(1−β2)dθJ(θ)⊗dθJ(θ)
3. ˆm<m1−βt1
4. ˆs<s1−βt2
5. θ<θ+ηˆm⊘√ˆs+ϵ
위 단계를 보면 Adam이 모멘텀 최적화와 RMSProp과 매우 비슷하다는 것을 알 수 있다. 단지, 단계 1에서 지수 감소 합 대신 지수 감소 평균을 계산하는 점이 다르지만 사실 상수 배인 것을 제외하면 동일하다(지수 감소 평균은 지수 감소 합의 1−β1배)
m과 s가 0으로 초기화되기 때문에 훈련 초기에는 0으로 치우치게 된다. 그래서 단계 3, 4에서 훈련 초기에 m과 s의 값을 증폭시키는 데 도움을 준다. 반복이 많이 진행되면 단계 3, 4의 분모가 1에 가까워지면서 거의 증폭되지 않는다.
모멘텀 감쇠 하이퍼파라미터 β1은 보통 0.9로 초기화하고, 스케일 감쇠 하이퍼파라미터 β2는 0.999로 초기화된다. 아래는 케라스에서 Adam 옵티마이저를 만드는 방법이다.
optimizer = keras.optimizers.Adam(lr=0.001, beta_1=0.9, beta_2=0.999)마지막으로 언급할 가치가 있는 Adam의 2가지 변종이 있다.
AdaMax
Adam의 단계 2를 보면 s에 그레이디언트 제곱을 누적한다(최근 그레이디언트에 더 큰 가중치 부여). 단계 5에선 s의 제곱근으로 파라미터 업데이트의 스케일을 낮추는데, 이는 다시 말하면 시간에 따라 감쇠된 그레이디언트의 l2 norm으로 파라미터 업데이트의 스케일을 낮추는 것이다. AdaMax는 l2 norm을 l∞ norm으로 바꾼다.
구체적으로 단계 2를 s<max(β2s,dθJ(θ))로 바꾸고 단계 4를 삭제한다. 단계 5에서 s에 비례하여 그레이디언트 업데이트의 스케일을 낮추며 이는 시간에 따라 감쇠딘 그레이디언트의 최댓값을 사용하는 것이다. 이 때문에 실전에서 AdaMax가 Adam보다 더 안정적이지만 일반적으로 Adam의 성능이 더 낫다. Adam이 잘 동작하지 않는다면 시도할 수 있는 옵티마이저 중에 하나이다.
Nadam
Nadam 옵티마이저는 Adam 옵티마이저에 네스테로프 기법을 더한 것이다. 종종 Adam보다 조금 더 빠르게 수렴한다고 알려져 있다.
지금까지 논의한 모든 최적화 기법은 1차 편미분(야코비안 - Jacobian)에만 의존한다. 최적화 이론에는 2차 편미분(헤시안 - Hessian, 야코비안의 편미분)을 기반으로 한 뛰어난 알고리즘이 있다. 하지만 이를 심층 신경망에 적용하기는 매우 어렵다. 하나의 출력마다 n개의 1차 편미분이 아니라 n2개의 2차 편미분을 계산해야 하기 때문이다(n은 파라미터 수). DNN은 전형적으로 수만 개의 파라미터를 가지므로 2차 편미분 최적화 알고리즘은 메모리 용량을 넘어서는 경우가 많고 계산이 너무 느리다.
11.3.6 학습률 스케줄링
훈련하는 동안 학습률을 감소시키는 전략을 학습 스케줄(learning schedule)이라고 한다.
1. 거듭제곱 기반 스케줄링(lower scheduling)
- 학습률을 반복 횟수 t에 대한 함수 η(t)=η0/(1+t/s)c로 지정
- 초기 학습률 eta0, 거듭제곱 수 c, 스텝 횟수 s는 하이퍼파라미터
- 학습률은 각 스텝마다 감소되어 s번 스텝 뒤에 학습률은 η0/2으로 줄어든다. s번 더 스텝이 진행 된 후 학습률은 η0/3으로 줄어들고 그다음 η0/4으로 줄어든다. 이렇게 처음에는 빠르게 감소하다가 점점 더 느리게 감소한다.
2. 지수 기반 스케줄링(exponential scheduling)
- 학습률을 η(t)=η00.1t/s로 설정
- 학습률이 s 스텝마다 10배씩 점차 줄어든다. 거듭제곱 기반 스케줄링이 학습률을 갈수록 천천히 감소시키는 반면 지수 기반 스케줄링은 s번 스텝마다 계속 10배씩 감소한다.
3. 구간별 고정 스케줄링(piecewise constant scheduling)
- 일정 횟수의 에포크 동안 일정한 학습률을 사용하고 그 다음 또 다른 횟수의 에포크 동안 작은 학습률을 사용하는 방식
4. 성능 기반 스케줄링(performance scheduling)
- 매 N 스텝마다 (조기 종료처럼) 검증 오차를 측정하고 오차가 줄어들지 않으면 λ배만큼 학습률 감소
5. 1사이클 스케줄링(1cycle scheduling)
- 훈련 절반 동안 초기 학습률 η0을 선형적으로 η1까지 증가시킨 후 나머지 절반 동안 선형적으로 학습률을 η0까지 다시 줄인다. 마지막 몇 번의 에포크는 학습률을 소수점 몇 째 자리까지 줄인다. 최대 학습률 η1은 최적의 학습률을 찾을 때와 같은 방식을 사용해 선택하고 초기 학습률 η0은 대략 10배 정도 낮은 값을 선택한다.
- 모멘텀을 사용할 때는 처음에 높은 모멘텀으로 시작해서 훈련의 처음 절반 동안 낮은 모멘텀으로 줄어든다. 다시 나머지 훈련 절반 동안 최댓값으로 되돌린다. 마지막 몇 번의 에포크는 최댓값으로 진행한다.
케라스에서 거듭제곱 기반 스케줄링은 아래와 같이 구현한다.
optimizer = keras.optim.SGD(lr=0.01, decay=1e-4) # decay는 s(학습률을 나누기 위해 수행할 스텝 수)의 역수
# 케라스에서 c=1로 가정지수 기반 스케줄링과 구간별 스케줄링 역시 간단하다. 지수 기반 스케줄링을 먼저 살펴보면 일단 현재 에포크를 받아 학습률을 반환하는 함수를 정의해야 한다.
def exponential_decay_fn(epoch):
return 0.01 * 0.1**(epoch / 20) # lr=0.01η0와 s를 하드코딩하고 싶지 않다면 이 변수를 설정한 클로저(closure)를 반환하는 함수를 만들 수 있다.
def exponential_decay(lr0, s):
def exponential_decay_fn(epoch):
return lr0 * 0.1**(epoch / s)
return exponential_decay_fn
exponential_decay_fn = exponential_decay(lr0=0.01, s=20)그 다음 이 스케줄링 함수를 전달하여 LearningRateScheduler 콜백을 만든다. 이후 콜백을 fit() 메서드에 전달한다.
lr_scheduler = keras.callbacks.LearningRateScheduler(exponential_decay_fn)
history = model.fit(X_train_scaled, y_train, [...], callbacks=[lr_scheduler])LearningRateScheduler은 에포크를 시작할 때마다 옵티마이저의 learning_rate 속성을 업데이트한다. 에포크마다 한 번씩 스케줄을 업데이트해도 보통 충분하다고 한다. 물론 에포크마다 스텝이 많다면 스텝마다 학습률을 업데이트하는 것이 좋다.
스케줄 함수는 두 번째 매개변수로 현재 학습률을 받을 수 있다. 다음과 같은 스케줄 함수는 이전 학습률에 0.11/20을 곱하여 동일한 지수 감쇠 효과를 낸다(여기선 에포크 1이 아니라 0에서부터 감쇠 시작).
def exponential_decay_fn(epoch, lr):
return lr * 0.1**(1 / 20) # 이전 구현과 달리 초기 학습률에만 의존하므로 적절히 설정해야 함모델을 저장할 때 옵티마이저와 학습률이 함께 저장된다. 새로운 스케줄 함수를 사용할 때도 아무 문제없이 훈련된 모델을 로드하여 중지된 지점부터 훈련을 계속 진행할 수 있다. 하지만 스케줄 함수가 epoch 매개변수를 사용하면 문제가 복잡해진다. 에포크는 저장되지 않고 fit() 메서드를 호출할 때마다 0으로 초기화된다. 중지된 지점부터 모델 훈련을 하면 매우 큰 학습률이 만들어져 모델의 가중치를 망가뜨릴 가능성이 높다. 하나의 방법은 epoch에서 시작하도록 fit() 메서드의 initial_epoch 매개변수를 수동으로 정하는 것이다.
구간별 고정 스케줄링을 위해선 아래의 스케줄 함수를 수용할 수 있다. 그 다음 지수 기반 스케줄링처럼 LearningRateScheduler 콜백을 만들어 fit() 메서드에 전달한다.
def piecewise_constant_fn(epoch):
if epoch < 5:
return 0.01
elif epoch < 15:
return 0.005
else:
return 0.001성능 기반 스케줄링을 위해선 ReduceLROnPlateau 콜백을 사용한다. 특정 에포크 동안 모델 성능이 개선 되지 않을 시 학습률을 동적으로 감소 시키는 것이다. 아래의 예시는 5번의 연속적인 에포크 동안 향상되지 않을 때마다 학습률에 0.5를 곱하는 것이다.
# ReduceLROnPlateau(monitor='val_loss', factor=0.1, patience=10, verbose=0, mode='auto', min_delta=0.0001, cooldown=0, min_lr=0)
lr_scheduler = keras.callbacks.ReduceLROnPlateau(factor=0.5, patience=5)
monitor: 모니터할 지표(loss 또는 평가 지표)
factor: 학습률을 줄일 인수(new_lr = lr * factor)
patience: 학습률을 줄이기 전에 모니터할 에포크 횟수
mode: {auto, min, max} 중 하나
- 모니터 지표가 감소해야 좋을 경우 min, 증가해야 좋을 경우 max, auto는 모니터 이름에서 유추
마지막으로 tf.keras 는 학습률 스케줄링을 위한 또 다른 방법을 제공한다. keras.optimizers.schedules 에 있는 스케줄 중에 하나를 사용해 학습률을 정의하고 이 학습률을 옵티마이저에 전달한다. 이렇게 하면 에포크가 아니라 매 스텝마다 학습률을 업데이트한다. 아래는 앞서 살펴본 exponential_decay_fn() 와 동일한 지수 기반 스케줄링을 구현하는 방법이다.
s = 20 * len(X_train) // 32 # 20번 에포크에 담긴 전체 스텝 수(배치 크기=32)
learning_rate = keras.optimizers.schedules.ExponentialDecay(0.01, s, 0.1)
optimizer = keras.optimizers.SGD(learning_rate)11.4 규제를 사용해 과대적합 피하기
신경망에서 널리 사용되는 규제 방법으로는 l1 및 l2 규제, 드롭아웃(dropout), 맥스-노름(max-norm) 규제 등이 있다.
11.4.1 l1과 l2 규제
아래는 규제 강도 0.01을 사용하여 l2규제를 적용하는 방법이다.
layer = keras.layers.Dense(100, activation='elu',
kernel_initializer='he_normal',
kernel_regularizer=keras.regularizers.l2(0.01))l2() 함수는 훈련하는 동안 규제 손실을 계산하기 위해 각 스텝에서 호출되는 규제 객체를 반환한다. 이 손실을 최종 손실에 합산된다. l1 규제는 keras.regularizers.l1() 을, l1과 l2 모두 필요하면 keras.regularizers.l1_l2() 를 사용한다.
일반적으로 네트워크의 모든 은닉층에 동일한 활성화 함수, 동일한 초기화 전략을 사용하거나 모든 층에 동일한 규제를 적용하므로 동일한 매개변수 값을 반복하는 경우가 많다. 이때 파이썬의 functools.partial() 함수를 톻해 기본 매개변수 값을 사용하여 함수 호출을 감싸는 방법을 사용하는 것이 좋다.
from functools import partial
RegularizedDense = partial(keras.layers.Dense,
activation='elu',
kernel_initializer='he_normal',
kernel_regularizer=keras.regularizers.l2(0.01))
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
RegularizedDense(300),
RegularizedDense(100),
RegularizedDense(10, activation='softmax', kernel_initializer='glorot_uniform')
])11.4.2 드롭아웃
드롭아웃은 2012년 제프리 힌턴이 제안했고, 니티시 스리바스타바(Nitish Srivastava)의 2014년 논문에서 더 자세히 설명하여 아주 잘 작동된다고 입증되었다.
매 훈련 스텝에서 각 뉴런(입력 뉴런은 포함, 출력 뉴런은 제외)은 임시적으로 드롭아웃될 확률 p를 가진다. 하이퍼파라미터 p를 드롭아웃 비율이라고 하고 보통 10%와 50% 사이를 지정한다.
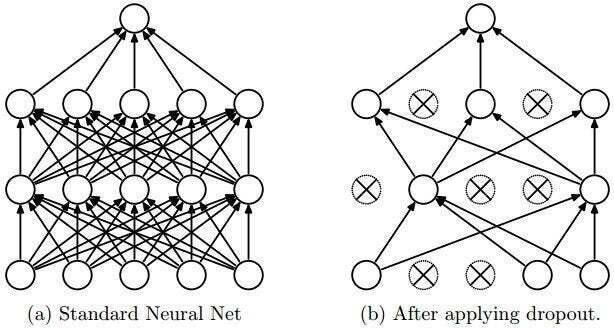
드롭아웃으로 훈련된 뉴런은 이웃한 뉴런에 맞춰 적응될 수 없으므로 가능한 한 자기 자신이 유용해져야 한다. 또 이런 뉴런들은 몇 개의 입력 뉴런에만 지나치게 의존할 수 없다. 모든 입력 뉴런에 주의를 기울여야 하기 때문에 입력값의 작은 변화에 덜 민감해진다. 결국 더 안정적인 네트워크가 되어 일반화 성능이 좋아진다고 할 수 있다.
드롭아웃의 능력을 이해하는 또 다른 방법은 각 훈련 스텝에서 고유한 네트워크가 생성된다고 생각하는 것이다. 개개의 뉴런이 있을 수도 없을 수도 있기 때문에 2N개의 네트워크가 가능하다(N=드롭아웃이 가능한 뉴런 수). 이는 아주 큰 값이라 같은 네트워크가 2번 선택될 가능성은 사실 거의 없으며 대부분 가중치를 공유하지만 그럼에도 매우 다르다고 볼 수 있다. 결과적으로 만들어진 신경망은 이 모든 신경망을 평균한 앙상블로 볼 수 있다.
(참고)
p=50로 하면 테스트하는 동안에는 하나의 뉴런이 훈련 때보다 (평균적으로) 2배 많은 입력 뉴런과 연결된다. 이를 보상하기 위해 훈련 뒤에 각 뉴런의 연결 가중치에 0.5를 곱할 필요가 있다. 일반적으로 말해서 훈련이 끝난 뒤 각 입력의 연결 가중치에 보존 확률(keep probability) 1−p를 곱해야 한다. 또는 훈련하는 동안 각 뉴런의 출력을 보존 확률로 나눌 수도 있다.
케라스에선 keras.layers.Dropout 층을 사용해 구현하고 훈련하는 동안 일부 입력을 랜덤하게 버린다(0으로 설정). 그다음 남은 입력을 보존 확률로 나눈다.
model =keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(300, activation='elu', kernel_initializer='he_normal'),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(100, activation='elu', kernel_initializer='he_normal'),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(10, activation='softmax')
])드롭아웃은 훈련하는 동안에만 활성화되므로 훈련 손실과 검증 손실을 비교하면 오해를 일으키기 쉽다. 따라서 (훈련이 끝난 후) 드롭아웃을 빼고 훈련 손실을 평가해야 한다.
많은 최신의 신경망 구조는 마지막 은닉층 뒤에만 드롭아웃을 사용한다. 드롭아웃을 전체에 적용하는 것이 너무 강하다면 이렇게 시도하는 것도 좋은 방법이다.
본 챕터의 초반에 소개했던 SELU 활성화 함수를 기반으로 자기 정규화하는 네트워크를 규제하고 싶다면 알파(alpha) 드롭아웃을 사용해야 한다. 이는 입력의 평균과 표준편차를 유지하는 드롭아웃의 한 변종이다.
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.AlphaDropout(rate=0.2),
keras.layers.Dense(300, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.AlphaDropout(rate=0.2),
keras.layers.Dense(100, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.AlphaDropout(rate=0.2),
keras.layers.Dense(10, activation="softmax")
])11.4.3 몬테 카를로 드롭아웃
야린 갤(Yarin Gal)과 주빈 가라마니(Zoubin Ghahramani)의 2016년 논문에서는 드롭아웃을 사용해야 할 몇 가지 이유를 소개했다.
1. 이 논문은 드롭아웃을 수학적으로 정의하여 드롭아웃 네트워크(즉 모든 가중치 층 이전에 Dropout층을 포함한 신경망)와 근사 베이즈 추론(approximate Bayesian inference) 사이에 깊은 관련성을 정립
2. 훈련된 드롭아웃 모델을 재훈련하거나 전혀 수정하지 않고 성능을 크게 향상시킬 수 있는 몬테 카를로 드롭아웃(Monte Carlo dropout, 이하 MC)이라 불리는 강력한 기법 소개
y_probas = np.stack([model(X_test_scaled, training=True) for sample in range(100)])
y_proba = y_probas.mean(axis=0)위 코드는 training=True 로 지정하여 Dropout 층을 활성화하고 테스트셋에서 100번의 예측을 만들어 쌓는 구조다. predict() 메서드는 샘플이 행이고 클래스가 열로 이루어진 행렬을 반환하는데, 이런 행렬이 100개 쌓았기 때문에 최종적으로 [100, 10000, 10] 크기의 행렬을 반환한다. 첫 번째 차원(axis=0)을 기준으로 평균내면 한 번의 예측을 수행했을 때와 같은 [10000, 10] 크기의 배열 y_proba를 얻게 된다.
드롭아웃으로 만든 예측을 평균내면 일반적으로 드롭아웃 없이 예측한 하나의 결과보다 더 안정적이다. 예를 들어 드롭아웃을 끄고 패션 MNIST 테스트셋에 있는 첫 번째 샘플의 모델 예측을 확인해보자.
np.round(model.predict(X_test_scaled[:1]), 2)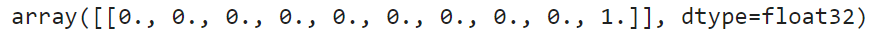
모델은 거의 확실하게 해당 이미지가 클래스9(앵클 부츠)에 속한다고 확신한다.
np.round(y_probas[:, :1], 2)
드롭아웃을 활성환 모델은 더 이상 확신하지 않는다. 이따금 클래스5(샌들)이나 7(스니커즈)로 생각한다. 아래는 첫 번째 차원으로 평균을 낸 MC 드롭아웃의 예측이다.
np.round(y_proba[:1], 2)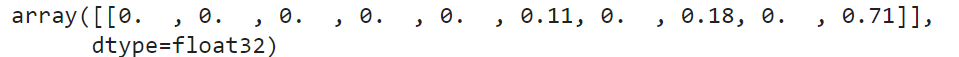
y_std = y_probas.std(axis=0)
np.round(y_std[:1], 2)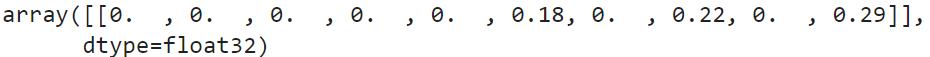
위의 분산 결과를 살펴보면 클래스9라고 예측한 결과에 꽤나 큰 분산이 존재함을 발견할 수 있다.
accuracy = np.sum(y_pred == y_test) / len(y_test)
accuracy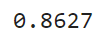
몬테 카를로 샘플의 숫자(위의 예시에선 100)는 튜닝할 수 있는 하이퍼파라미터이다. 이 값이 높을수록 예측과 불확실성 추정이 더 정확해지지만 그만큼 예측 시간도 더 걸리게 된다. 또한 일정 샘플 수가 넘어서면 성능이 크게 향상되지 않는다.
모델이 훈련하는 동안 다르게 작동하는 (BatchNormalization 층 등) 층을 가지고 있다면 앞선 방법처럼 훈련 모드를 강제로 설정해선 안 된다. 대신 Dropout 층을 다음과 같은 MCDropout 클래스로 바꿔줘야 한다.
class MCDropout(keras.layers.Dropout):
def call(self, inputs):
return super().call(inputs, training=True)MC 드롭아웃은 드롭아웃 모델의 성능을 높여주고 더 정확한 불확실성 추정을 제공하는 기술이다. 물론 훈련하는 동안은 일반적인 드롭아웃처럼 수행하기 때문에 규제처럼 작동한다.
11.4.4 맥스-노름 규제
맥스-노름 규제는 각각의 뉴런에 대해 입력의 연결 가중치 w가 ∥w∥2≤r이 되도록 제한한다(r$은 맥스-노름 하이퍼파라미터).
맥스-노름 규제는 전체 손실 함수에 규제 손실 항을 추가하지 않는다. 대신 일반적으로 매 훈련 스텝이 끝나고 ∥w∥2를 계산하고 필요하면 w의 스케일을 조정한다(w<wr∥w∥2). r을 줄이면 규제의 양이 증가하여 과대적합을 감소시키는 데 도움이 된다. 맥스-노름 규제는 (배치 정규화를 사용하지 않았을 때) 불안정한 그레이디언트 문제를 완화하는 데 도움을 줄 수 있다.
keras.layers.Dense(100, activation='elu', kernel_initializer='he_normal',
kernel_constraint=keras.constraints.max_norm(1.))max_norm() 함수는 기본값이 0인 axis 매개변수가 있다. axis=0 을 사용하면 맥스-노름 규제는 각 뉴런의 가중치 벡터에 독립적으로 적용되는데, CNN에 맥스-노름을 사용하려면 axis 매개변수를 적절하게 지정해야 한다.
- Understanding the difficulty of training deep feedforward neural networks [본문으로]
- Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs) [본문으로]
- Self-Normalizing Neural Networks [본문으로]
- Fixup Initialization: Residual Learning Without Normalization [본문으로]
- 가속되는 물체가 저항 때문에 더는 가속되지 않고 등속도 운동을 하게 될 때의 속도 [본문으로]
- 1번 식에 좌우변을 같게 놓고 정리하면 됨 [본문으로]
'문돌이 존버 > 데이터 분석' 카테고리의 다른 글
| 핸즈온 머신러닝 2 복습하기(챕터 15: RNN과 CNN을 사용해 시퀀스 처리하기) (1) | 2023.10.05 |
|---|---|
| 핸즈온 머신러닝 2 복습하기(챕터 14: 합성곱 신경망을 사용한 컴퓨터 비전) (0) | 2022.05.02 |
| 버트(BERT) 개념 간단히 이해하기 (2) | 2021.11.17 |
| 트랜스포머(Transformer) 간단히 이해하기 (2) (2) | 2021.11.11 |
| 트랜스포머(Transformer) 간단히 이해하기 (1) (1) | 2021.11.11 |



