본 글은 여러 블로거님들의 훌륭한 지식을 참고하여 작성하였습니다. 감사드립니다.
힙(Heap)
오늘은 자료구조 중 힙에 대해 스스로 정리하고 다시 이해해보려고 한다.
- 힙의 세 가지 큰 특징(Max heap 기준)
1. 루트 노드가 항상 최댓값을 지님 -> 이를 Heap propoerty라 함
2. 반드시 완전 이진 트리(complete binary tree)여야 함
3. 최대 힙 내의 임의의 노드를 루트로 하는 서브트리 또한 최대 힙
참고로 포화 이진 트리(perfect binary tree)와 완전 이진 트리는 아래 그림과 같다.


포화 이진 트리: 루트로부터 시작해서 맨 마지막 레벨까지 모든 노드가 정확히 2개씩의 자식 노드를 가지도록 꽉 채워진 트리(노드 수가 2k−1일 때만 가능)
완전 이진 트리: 루트로부터 시작해서 가능한 지점까지 모든 노드가 정확히 2개씩의 자식 노드를 가진다. 노드 수가 맞지 않아 포화 이진 트리를 만들 수 없으면 맨 마지막 레벨은 왼쪽부터 채워나간다.
BST(binary search tree)는 원소들이 완전히 크기 순서로 정렬되어 있어, 순회(traverse)를 돌면 데이터를 정렬된 순서로 출력할 수 있다. 반면, 힙은 크기 순으로 정렬되어 있지 않고 오직 루트 노드가 최댓값이다. 따라서 탐색을 하기에는 적절하지 않은 자료구조라고 할 수 있다.
대신 삽입 및 삭제 연산이 BST보다 빠르기 때문에 장점이 된다. 기본적으로 트리 구조라 연산의 시간 복잡도는 O(logN)이지만 완전 이진 트리여야 하므로 모든 삭제 및 삽입 연산이 배열 가장 끝에서 발생한다.(최선의 경우 시간 복잡도는 Θ(1))
힙은 어레이와 연계하여 이해하면 쉽다. 사실상 어레이는 완전 이진 트리로 볼 수 있다.

위에선 루트 노드를 배열 인덱스 1로 본 것이고, 0으로 본다면 자식 및 부모 노드의 번호는 아래와 같을 것이다.
왼쪽 자식의 번호: 2 * m + 1
오른쪽 자식의 번호: 2 * m + 2
부모 노드의 번호: m-1 // 2
먼저 힙의 삽입(insertion)부터 살펴보도록 한다.
class MaxHeap:
def __init__(self):
self.data = [None]
def insert(self, item):
self.data.append(item)
i = len(self.data) - 1 # 새로운 원소에 해당하는 인덱스
while i > 1:
if self.data[i] > self.data[(i // 2)]:
self.data[i], self.data[(i // 2)] = self.data[(i // 2)], self.data[i]
i = i // 2
else:
break먼저, 추가할 데이터를 마지막에 넣고 이 원소를 부모 노드와 대소 비교하며 "최대 힙 내의 임의의 노드를 루트로 하는 서브 트리 또한 최대 힙"이라는 규칙을 만족하도록 할 것이다.
이는 서브 트리 내에서 부모 노드가 가장 큰 값을 지녀야 함을 뜻한다.
다음은 삭제(deletion) 과정이다.
def remove(self):
if len(self.data) > 1:
self.data[1], self.data[-1] = self.data[-1], self.data[1]
data = self.data.pop()
self.maxHeapify(1)
else:
data = None
return data먼저, 루트 노드에 있는 값을 힙 가장 끝의 노드와 교환한다. 힙 가장 끝 노드에 Max 원소가 위치하고 이때 pop() 하면 힙 크기가 1 줄어듦과 동시에 원하는 값이 리턴된다.
이후 힙의 3가지 규칙을 지키기 위해 현재 루트 노드에 있는 값을 적절한 위치로 옮겨야 한다. 즉 자식 노드(왼쪽, 오른쪽)와 대소 비교하며 이동해야 하는 것이다. 이를 행하는 함수가 maxHeapify() 이다.
def maxHeapify(data, idx, heap_size): # 주어진 자료구조를 Heap property를 만족하도록 하는 연산
left = 2 * idx
right = (2 * idx) + 1
largest = idx
# 왼쪽 자식이 존재하는지, 루트 노드 값이 왼쪽 자식 노드보다 작은지 확인
if left < len(data) and data[idx] < data[left]:
largest = left # 작은 값은 왼쪽 노드가 됨
# 오른쪽 자식이 존재하는지, 루트 노드 값이 오른쪽 자식 노드보다 작은지 확인
if right < len(data) and data[idx] < data[right]:
largest = right
if largest != idx:
data[idx], data[largest] = data[largest], data[idx]
maxHeapify(data, largest, heap_size) # Heap property를 만족할 때까지 재귀 반복Min heap의 경우 largest가 아니라 smallest, 즉 루트 노드가 자식 노드들보다 큰 지 확인하면 된다. 루트 노드가 가장 작은 수여야 함을 보장해야 하는 것이다.
위의 maxHeapify 는 결국 깊이(level)에 따라 시간 복잡도가 걸리게 되는데, 최악의 경우 처음 선택된 노드 값이 가장 작아 총 깊이인 h(=log2n)까지 이르러야 할 수 있다. 결과적으로 시간 복잡도는 O(logn)이 된다.
힙의 삽입과 삭제 역시 시간 복잡도는 O(logn)이 된다.
삽입: 삽입하는 데 드는 연산 O(1), 해당 노드를 heapify 하는 데 O(logn)이 들어 전체적으로는 O(logn)이 된다.
삭제: 역시 삭제하는 데 드는 연산 O(1), 배열의 마지막 노드를 삭제 위치로 옮기는 연산 O(1), 해당 노드를 heapify하는 데 드는 연산 O(logn)으로, 전체적으로 O(logn)이 된다.
Build heap
임의의 숫자들을 Max heap으로 구성하는 일련의 연산 과정을 build heap() 이라고 한다. 가장 간단하게 구현하는 방법은 비어있는 힙에 요소들을 insert 연산을 수행해 힙을 만들어가는 것이다.
이렇게 되면 새로 삽입해야 할 노드 수가 n개일 때 총 insert 연산을 n번 반복 수행하게 된다. 그리고 위에서 삽입 연산은 O(logn) 시간 복잡도를 가지기 때문에 이 방법은 결과적으로 O(nlogn)의 시간 복잡도를 가진다.
하지만 이보다 더 좋은 방법이 있다. 주어진 배열을 완전 이진 트리 형태로 나열하고 배열의 개수를 2로 나눈 몫을 인덱스로 하는 노드부터 차례대로 heapify()를 수행하는 것이다.
배열: [12, 30, 6, 7, 4, 13, 8, 11, 50, 24, 2, 5, 10]
개수: 13
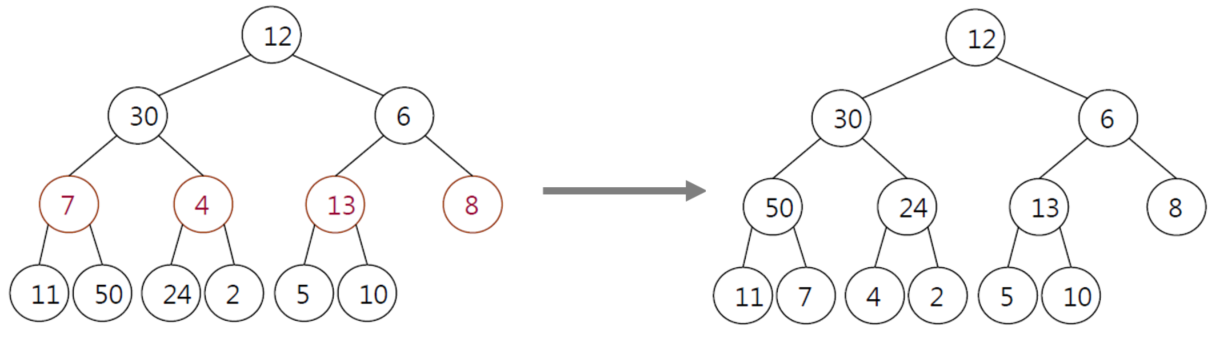
위에서 배열의 개수를 2로 나눈 몫은 6이고, 이에 해당하는 노드는 "8"이다. 여기서 "8 -> 13 -> 4 -> 7" 순서대로 위에서 아래로 heapify()를 수행한다.
8 -> 자식노드가 없기 때문에 heapify() 종료
13 -> 자식노드인 5와 10보다 크기 때문에 Heap property 만족, 따라서 heapify() 종료
4 -> 왼쪽 자식노드인 24보다 작기 때문에 Heap property 만족 X, 따라서 4와 24 위치 바꿈
새로운 위치의 4는 자식노드가 없기 때문에 heapify() 종료
7 -> 자식노드인 11과 50보다 작기 때문에 Heap property 만족 X, 따라서 7과 50 위치 바꿈
새로운 위치의 7은 자식노드가 없기 때문에 heapify() 종료
이후 노드 "6 -> 30 "순서대로 heapify()를 수행한다. 마지막으로 "루트 노드"를 대상으로 heapify()를 수행한다.
위의 계산복잡성을 따져보면, 1개 노드를 heapify() 하는 데 필요한 계산량이 O(logn)이고, n/2개 노드에 대해 수행해야 하기 때문에 전체적으로 O(nlogn)이 된다. 하지만 더 생각해볼 문제가 있는데 아래 그림을 살펴보자.
모든 레벨의 모든 노드가 꽉 차 있는 포화 이진 트리
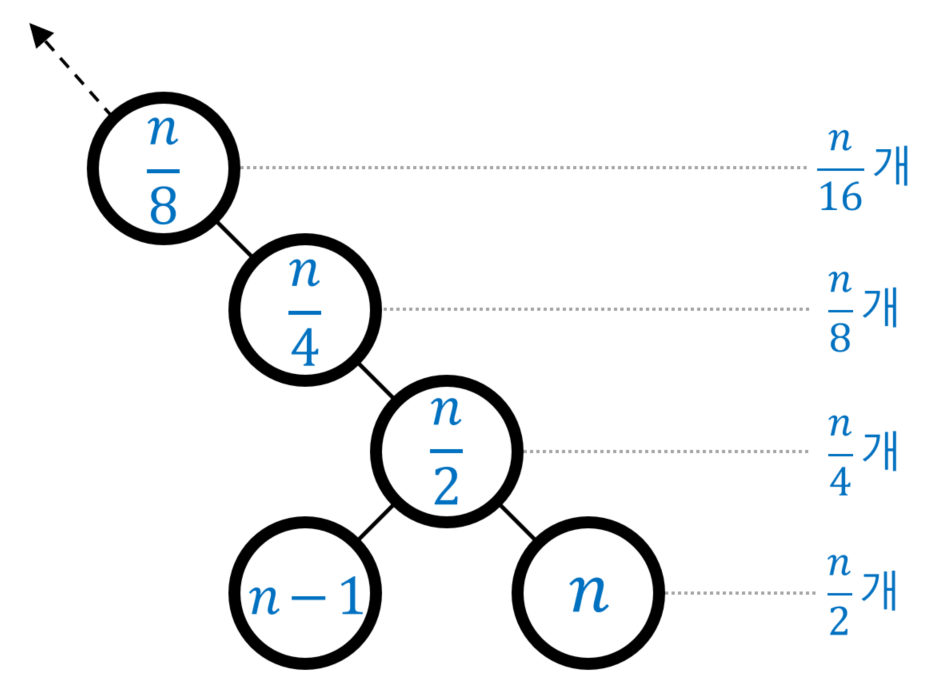
위 그림에서 노드 안 숫자들은 노드 수가 n개인 이진트리를 배열로 표현했을 때의 인덱스다. 엄밀히 따지면, 위 조건에 있는 "모든 레벨의 모든 노드가 꽉 차 있는 포화 이진 트리"의 경우 n은 홀수만 가능하다. 따라서 한 레벨에 노드 수가 n/2개, n/4개가 될 수 없으며 이는 홀수인 n에 1을 더한 값을 생각하면 된다.
즉 n이 7개이면 8이라 생각하고 위의 그림을 이해하면 된다. 그러면 위에서 노드에 적힌 인덱스나 한 레벨의 노드 개수가 납득이 간다.
이러한 build heap() 의 계산복잡성은 수행 대상의 노드가 전체 트리에서 차지하는 높이 및 수행 대상 노드 수에 비례한다. 높이(=레벨)는 잎새 노드까지의 엣지 수를 의미하는데, 예를 들어, 위 그림에서 인덱스가 n/2인 노드의 높이는 "1"이 된다.
종합적(=평균적)으로 살펴보면 시간 복잡도를 나타내는 식은 아래와 같다.
(0∗n/2)+(1∗n/4)+(2∗n/8)+...+(h∗1)
해당 식을 Taylor 급수를 사용하면 O(n)의 시간 복잡도를 갖는다고 한다. 증명 과정은 참고로 첨부하겠다.
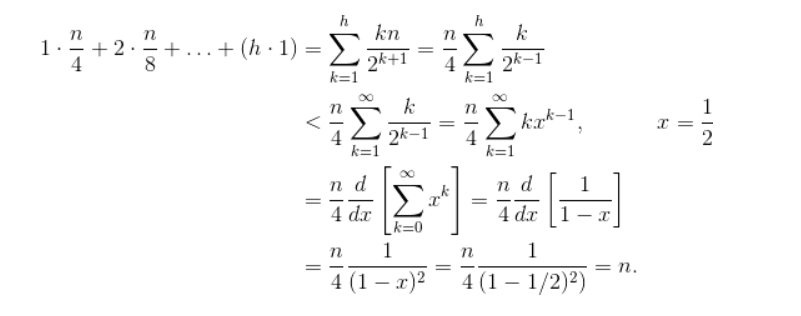
Heap sort
힙 정렬을 위해선 우선 주어진 데이터를 가지고 먼저 Max heap을 구성해야 한다.
unsorted = [16, 4, 10, 14, 7, 9, 3, 2, 8, 1]
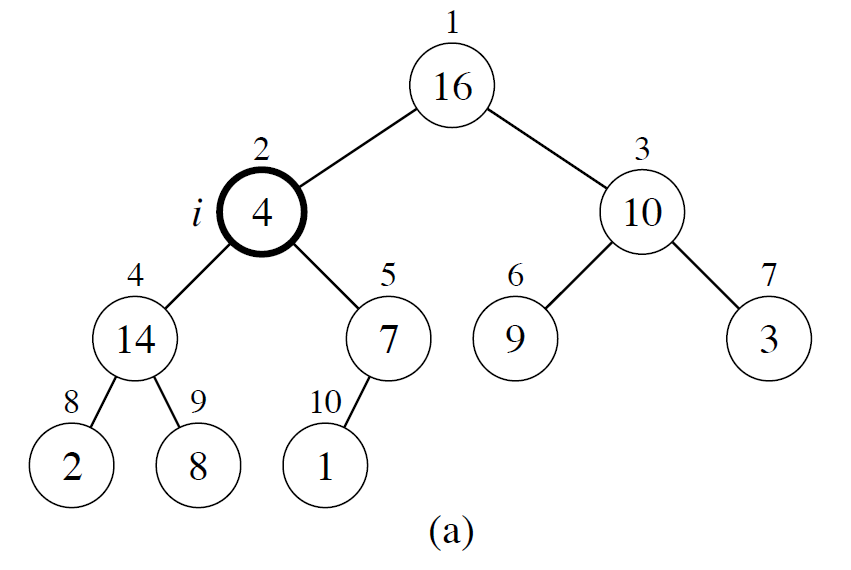
1. heapify() 의 시작점은 데이터 개수의 절반에 해당하는 인덱스 위치의 노드로 위에선 "노드 7"이 된다. 자식노드와 비교했을 때 Heap property를 만족하기 때문에 종료한다.
2. 이후 살펴볼 "노드 14"는 자식노드보다 크기 때문에 마찬가지로 종료한다.
3. 이후 살펴볼 "노드 10"은 자식노드보다 크기 때문에 종료한다.
4. 이후 살펴볼 "노드 4"는 Heap property를 만족하지 않기 때문에 자식노드인 "노드 14"와 자리를 바꾼다.
5. 원래 "노드 14"자리로 온 "노드 4"를 다시 살펴보고, 오른쪽 자식 노드로 인해 Heap property를 만족하지 않기 때문에 "노드 8"과 자리를 바꾼다.
위의 5단계 과정을 거치면 아래 그림이 나온다. 이때 "노드 4"는 자식노드가 없기 때문에 heapify() 를 종료하고 마지막으로 첫 번째(=루트) 노드에 대해 연산을 실행할 차례이다. "노드 16"은 Heap property를 만족하기 때문에 모든 연산을 종료하게 된다.
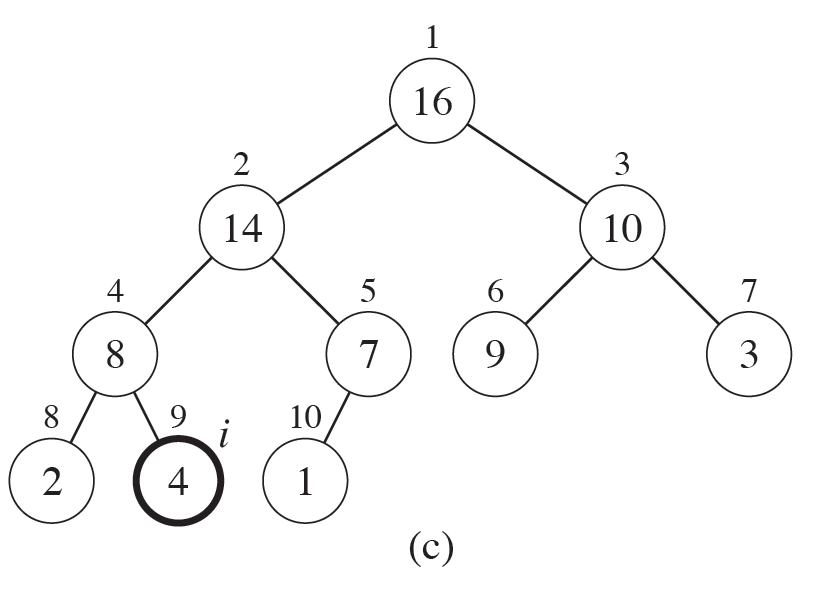
이로써 Max heap을 구성하였고 unsorted는 아래와 같이 변경되었다.
unsorted = [16, 14, 10, 8, 7, 9, 3, 2, 4, 1]
본격적인 힙 정렬은 아래 방법으로 수행한다.
1. 주어진 원소들로 Max heap 구성
2. Max heap의 루트노드(=최댓값)와 말단노드를 교환
3. 새 루트노드에 대해 Max heap 구성
4. 원소 갯수만큼 2단계와 3단계 반복 수행
def heap_sort(unsorted):
heap_size = len(unsorted)
# BUILD-MAX-HEAP (A) : 위의 1단계
# 인덱스 : (n을 2로 나눈 몫-1) ~ 0
# 최초 힙 구성시 배열의 중간부터 시작하면 이진트리 성질에 의해 모든 요소값을 서로 한번씩 비교할 수 있게 됨 : O(n)
for idx in range(n // 2 - 1, -1, -1):
heapify(unsorted, idx, heap_size)
# Recurrent (B) : 2~4단계
# 한번 힙이 구성되면 개별 노드는 최악의 경우에도 트리의 높이(logn)만큼의 자리 이동을 하게 됨
# 이런 노드들이 n개 있으므로 : O(nlogn)
for idx in range(n - 1, 0, -1):
unsorted[0], unsorted[idx] = unsorted[idx], unsorted[0]
heapify(unsorted, 0, idx)
return unsortedunsorted = [1, 2, 3, 4, 7, 8, 9, 10, 14, 16]
위와 같은 힙 정렬의 시간 복잡도는 A와 B를 합친 O(n)+O(nlogn)이며 결과적으로는 O(nlogn)이 된다.
참고
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=leeinje66&logNo=221622360256
build heap 시간복잡도 O(n) 이해하기 :: Paris on the chair (tistory.com)
https://ratsgo.github.io/data%20structure&algorithm/2017/09/27/heapsort/
'문돌이 존버 > 프로그래밍 스터디' 카테고리의 다른 글
| (프로그래머스 연습 문제 풀이) 문자열 압축 (0) | 2021.07.19 |
|---|---|
| (프로그래밍 힙(Heap) 문제 풀이) 더 맵게 (0) | 2021.07.19 |
| (프로그래머스 깊이/너비 우선 탐색 문제 풀이) 타겟 넘버 (0) | 2021.07.18 |
| (leetcode 문제 풀이) Merge Two Sorted Lists (0) | 2021.07.18 |
| (leetcode 문제 풀이) Valid Parentheses (0) | 2021.07.16 |



