누적 지역 효과(Accumulated Local Effects, 이하 ALE)는 특성값이 머신러닝 모델의 예측에 평균적으로 얼마나 영향을 미쳤는지 설명합니다. ALE 그래프는 더 빠르고 덜 편향적으로 PDP를 대체할 수 있습니다.
동기와 직관적 이해
머신러닝 모델의 특성들이 상관관계를 가지고 있다면, PDP는 신뢰할 수 없습니다(이는 PDP를 설명할 때도 이야기한 내용). 다른 특성과 강한 상관관계를 가진 하나의 특성에 대해 PDP를 계산하려면 비현실적인 가공(artificial) 데이터 인스턴스의 평균 예측도 포함됩니다. 이는 추정된 특성값 효과를 크게 편향시킬 수 있습니다. 방 개수와 거실 크기에 따라 집값을 예측하는 머신러닝 모델의 PDP를 구한다고 가정해보죠.
PDP를 구하는 단계는 아래와 같습니다.
1. 특성 선택
2. 그리드(=눈금) 정의
3. 그리드 값: a) 특성값을 그리드 값으로 대체하고, b) 평균 예측값으로 대체
4. 곡선 그리기
PDP의 첫 번째 그리드 값, 예를 들어 30m2라고 했을 때 모든 인스턴스의 거실 크기를 30m2라고 대체합니다. 방이 10개인 집의 거실 크기도 30m2라고 하는 것이죠. 매우 비현실적이지만 PDP는 특성값 효과 추정에 포함시키고 모든 것이 정상이라고 간주합니다.

x1와 x2는 강한 상관관계를 보입니다. x1이 0.75일 때의 특성값 효과를 구하기 위해 PDP는 모든 인스턴스의 x1 값을 0.75로 대체했습니다. 이는 x1=0.75인 값에서 보이는 수직선(주변 분포)입니다. PDP는 평균 효과를 계산하는 데 이와 같은 비현실적인 x1 및 x2 조합을 사용합니다.
그렇다면 어떻게 특성들 간 상관관계를 고려한 특성 효과 추정치를 얻을 수 있을까요? 먼저 특성값의 조건부 분포에 대한 평균을 계산할 수 있습니다. 즉 x1의 그리드 값에서 x1와 비슷한 값을 가진 인스턴스들의 예측을 평균냅니다. 조건부 분포를 사용하여 특성값 효과를 계산하는 것을 주변 분포(Marginal Plot) 혹은 M-Plot이라고 부릅니다.
잠깐! 여기서 이야기하고자 하는 것이 M-Plot이 아니라 ALE Plot입니다. M-Plot의 경우 30m2 크기의 모든 집에 대한 예측을 평균내면, 상관관계로 인하여 거실 크기와 방 개수의 결합 효과(combination effect)를 추정하게 됩니다. 거실 크기가 집값 예측에 영향을 미치지 않고, 오직 방 개수만 영향을 미친다고 가정해봅시다. 방 개수는 거실 크기와 함께 증가하기 때문에 M-Plot은 여전히 거실 크기가 예측값을 증가시키는 요인이라고 나타낼 것입니다.

M-Plot은 조건부 분포에 대해 평균을 냅니다. 위 그래프에선 x1=0.75일 때 x2의 조건부 분포를 나타냅니다. 지역(local) 예측에 대해 평균을 계산하는 것은 2개 특성 효과를 섞는 방향으로 이끕니다.
M-Plot은 비현실적인 데이터 인스턴드들의 예측에 대해 평균을 내지 않으나 상관관계가 있는 특성들의 영향을 모두 섞어버립니다. ALE Plot은 특성의 조건부 분포를 기반으로 하되 평균을 내지 않고 예측값과의 차이를 계산함으로써 이를 해결합니다.
거실 크기가 30m2일 때 ALE는 30m2 주변의 모든 집들을 사용하여 해당 집들이 31m2이라고 가정할 때와 29m2라고 가정할 때의 예측치 차이를 구합니다. 이렇게 함으로써 상관관계를 가진 특성들의 효과를 섞지 않고 거실 크기의 순수 효과를 알 수 있습니다. 차이를 사용하는 것은 다른 특성 효과의 개입을 막을 수 있습니다.
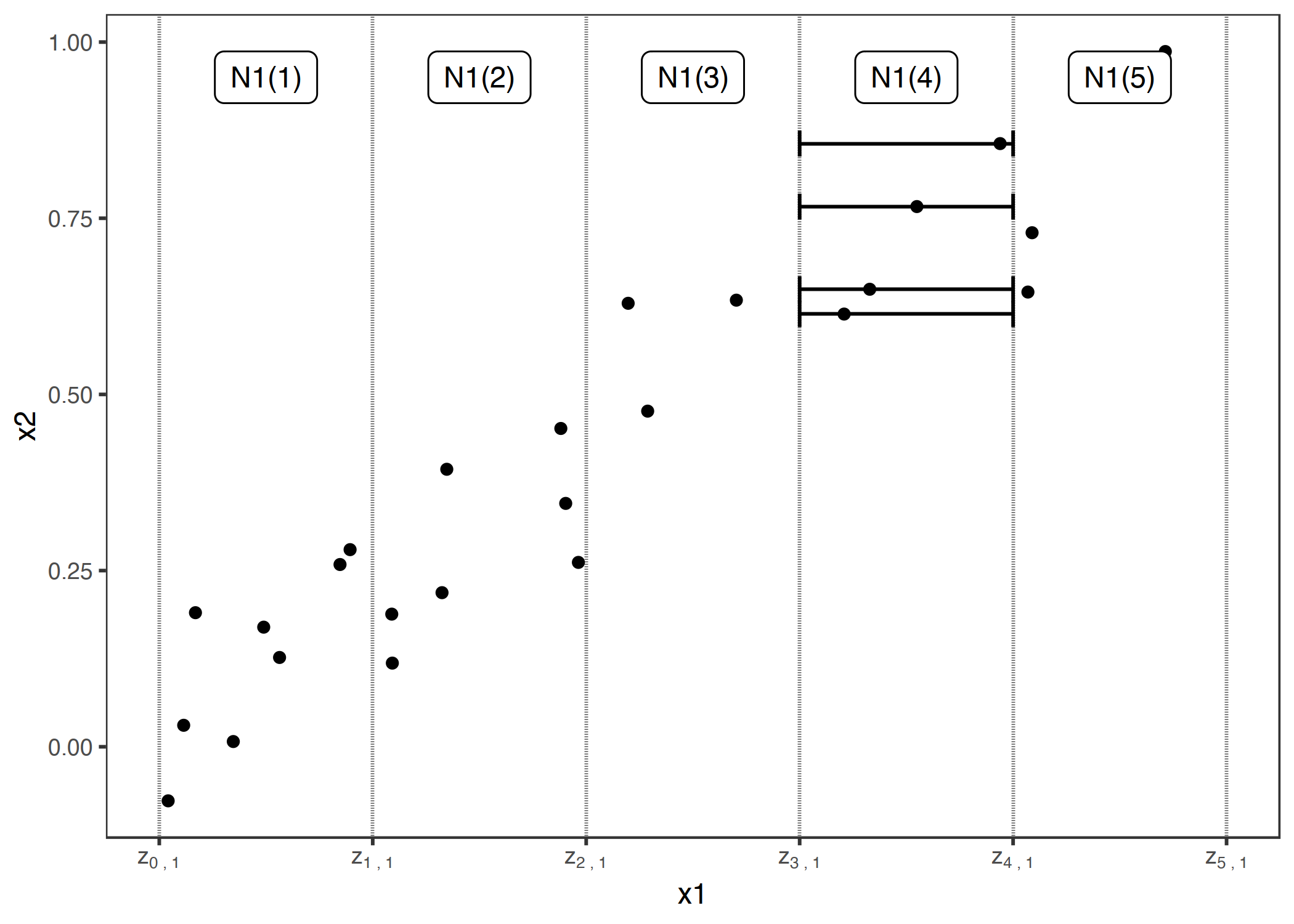
먼저, 특성을 몇 개의 구간(수직선으로 표시)으로 나눕니다. 각 구간에 있는 데이터 인스턴스들에 대해 상한 및 하한값으로 대체했을 때의 예측치 차이를 계산합니다. 이 차이값이 이후에 누적되고 중심화되면서 ALE 곡선을 만들어냅니다.
각 그래프 타입(PDP, M, ALE)이 하나의 특성의 특정 그리드 값 v의 효과를 어떻게 계산하는지 요약하자면 아래와 같습니다.
PDP: 각 데이터 인스턴스가 하나의 특성값 v를 가질 때 모델 예측의 평균값을 보여준다. 특성값 v가 모든 데이터 인스턴스에 대해 현실 가능성이 있는지는 상관하지 않는다.
M-Plot: 각 데이터 인스턴스가 하나의 특성값 v를 가질 때 모델 예측의 평균값을 보여준다. 특성의 효과는 해당 특성 때문일지도 혹은 상관관계를 가진 다른 특성 때문일지 모른다.
ALE: 특성값 v 주변의 작은 "윈도우(window)" 내에 있는 데이터 인스턴스들을 기반으로 모델 예측이 어떻게 변하는지 보여준다.
이론
PDP, M-Plot, ALE 모두 복잡한 예측 함수 f를 1개 혹은 2개 특성에 의존하는 함수로 변환합니다. 하지만 1) 예측치의 평균을 구하는지, 예측치의 차이를 구하는지가 다르고, 2) 주변 분포에 대해 평균을 내는지, 조건부 분포에 평균을 내는지가 다릅니다.
PDP는 주변 분포에 대해 예측한 것을 평균내는 방식입니다.
ˆfxs,PDP(xs)=Exc[ˆf(xs,Xc)]
=∫xcˆf(xs,xc)P(xc)dxc
예측 함수 f의 결과인 특성값 xs은 xc의 모든 특성에 대해 평균을 낸 값입니다. 평균을 낸다는 것은 집합 C의 특성들에 대해 주변 기대값 E를 계산하는 것입니다. 이는 확률 분포에 의해 가중된(weighted) 예측값에 대한 적분입니다. 어려운 테크닉처럼 들리지만 사실은 주변 분포에 대한 기대값을 계산하기 위해단순히 모든 데이터 인스턴스들이 집합 S의 특성값에 대해 특정 그리드 값을 갖도록 하는 것입니다. 그리고 조정된 데이터셋의 예측을 평균화하는 것이죠. 해당 과정은 특성들의 주변 분포에 대한 평균을 보장합니다.
M-Plot은 조건부 분포에 대한 예측을 평균냅니다.
ˆfxs,M(xs)=EXc|Xs[ˆf(Xs,Xc)|Xs=xs]
=∫xcˆf(xs,xc)P(xc|xs)dxc
PDP와 유일하게 다른 점은 관심있는 특성의 모든 그리드 값에 주변 분포 대신 조건부 분포에 대한 평균을 내는 것입니다. 이는 이웃(범위)을 정의해야 함을 의미하는데, 예를 들어 집값 예측에 30m2 거실 크기가 미치는 효과를 계산하기 위해 28 ~ 32m2 크기의 집들에 대한 예측을 평균내는 것입니다.
ALE Plot은 예측 변화량을 평균내고 그리드에 이를 누적하는 것입니다.
ˆfxs,ALE(xs)=∫xsz0,1EXc|Xs[ˆfS(Xs|Xc)|Xs=zs]dzs −constant
=∫xsz0,1∫xcˆfS(zs,xc)P(Xc|zs)dxcdzs −constant
위의 식은 M-Plot과 3가지 차이점을 드러냅니다. 첫 번째는 예측 자체를 평균내지 않고, 예측 변화량의 평균을 냅니다. 변화량은 기울기(gradient)로 정의됩니다(하지만 실제 계산에선 구간에 따른 예측 차이로 대체).
ˆfS(xs,xc)= δˆf(xs,sc)δxs
두 번째는 z에 대한 추가 적분입니다. 집합 S에서 특성값의 범위에 걸쳐 지역적 기울기를 누적하는데, 이를 통해 특성값이 예측에 미치는 영향을 알 수 있습니다. 실제 계산에서는 z값들이 예측값의 변화량을 계산하는 구간 눈금으로 대체됩니다. 예측값을 바로 평균내는 대신 ALE는 특성값 S를 조건으로 예측값 차이를 계산하고 효과를 추정하기 위해 S에 대한 미분값을 통합합니다.
하지만 일반적으로 미분과 적분은 서로를 상쇄시킵니다. 왜 여기선 이러한 계산법이 적용된 것일까요? 미분(또는 구간 차이)은 관심있는 특성의 영향을 분리하고 상관관계를 가진 특성값의 영향을 막아냅니다.
세 번째 차이점은 결과에서 상수(constant)를 빼는 것입니다. 이 단계는 데이터에 대한 평균 효과가 0이 되도록 ALE Plot을 중심화하는 것입니다.
한 가지 남아있는 문제점은 일부 모델들(예: 랜덤포레스트)의 경우 변화량을 정의하는 기울기가 존재하지 않습니다. 뒤에서 보겠지만 실제 계산은 기울기 없이 구간을 이용합니다.
추정
먼저, ALE Plot이 단일 수치 특성값을 어떻게 추정하는지, 이후 2가지 수치 특성값을 그리고 단일한 카테고리 특성값을 추정하는지 설명하겠습니다. 지역적 효과를 추정하기 위해 특성값을 많은 구간으로 나누고 예측의 변화량을 계산합니다. 이는 기울기를 근사하며 기울기가 없는 모델에도 적용 가능합니다.
중심화되지 않은 효과를 우선 예측해보겠습니다.
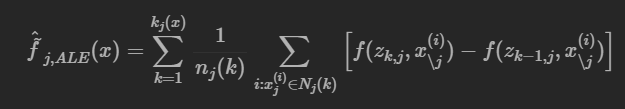
ALE의 핵심은 예측값의 차이를 계산하는 것이며, 이때 관심있는 특성값을 그리드 값 z로 대체합니다. 예측값의 차이는 특정 구간의 개별 인스턴스에 대해 특성값이 갖는 효과입니다. 오른쪽 합(summation) 공식은 이웃 Nj(k)로 나타나는 구간 내에 있는 모든 인스턴스들의 효과를 합산하는 것입니다. 해당 구간의 예측값 변화를 평균내기 위해 구간 내 인스턴스 개수로 합한 값을 나누어줍니다. 이 평균이 ALE에서 말하는 Local이 되는 것입니다. 왼쪽 합 공식은 모든 구간에 걸쳐 평균 효과를 누적한다는 것을 의미합니다. 예를 들어, 3번째 구간에 있는 특성값의 ALE는 1, 2, 3번 구간의 효과 합을 나타냅니다. 이것이 ALE의 Accumulated가 되는 것입니다.
이제 효과는 중심화되어 평균 효과가 0이 됩니다.
ˆfj,ALE(x)=ˆ∼fj,ALE(x)−1n∑ni=1ˆ∼fj,ALE(x(i)j)
ALE 값은 데이터의 평균 예측에 비해 일정한 값에서 갖는 특성값의 주효과(main effect)로 해석할 수 있습니다. 예를 들어, xj=3에서 ALE 추정치가 -2라면 j번째 특성값이 3일 때의 예측이 평균 예측에 비해 2만큼 낮다는 것을 의미합니다.
특성값 분포의 사분위수(quantile)는 구간을 정의하는 그리드로 사용됩니다. 사분위수는 각 구간마다 동일한 개수의 데이터 인스턴스를 보장합니다. 다만 구간마다 다른 길이를 가질 수 있다는 단점이 존재하며, 이는 관심있는 특성이 매우 왜곡되었다면(skewed) 이상한 ALE Plot을 생성하게 됩니다.
2개 특성 간 상호작용에 대한 ALE Plot
ALE Plot은 2개 특성 간 상호작용 효과를 나타낼 수도 있습니다. 계산 원리는 단일 특성 때와 동일하지만 2차원에서 효과를 누적해야 하므로 구간이 아닌 직사각형 셀(cell)을 사용합니다. 또한 전체 평균 효과에 대한 조정 이외에도 2개 특성값의 주요 효과에 대해서도 조정해야 합니다. 이는 2개 특성값에 대한 ALE는 주효과를 제외한 2차 효과(second-order effect)를 추정함을 의미합니다. 다시 말해 오직 2개 특성값의 추가적인 상호작용 효과만 나타낸다는 것입니다.
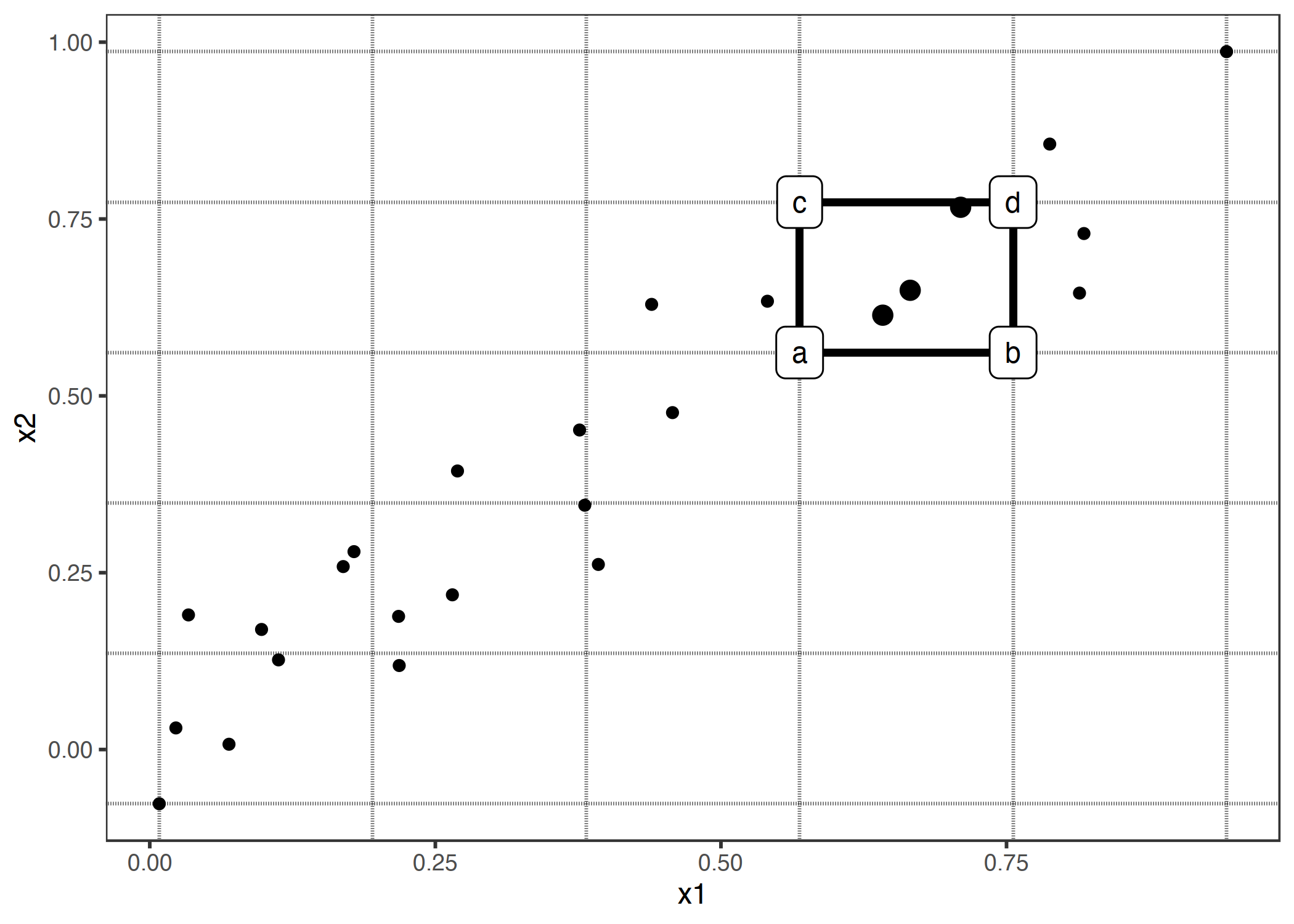
매 그리드 셀마다 모든 인스턴스에 대해 2차 차이(difference)를 구합니다. 먼저 x1과 x2 값을 셀 코너의 값들로 대체합니다. 위 그래프에서 a, b, c, d가 조작된 인스턴스의 "코너" 예측을 나타낸다면 2차 차이는 (d - c) - (b - a)입니다. 각 셀의 2차 차이 평균은 그리드마다 누적되고 중심화됩니다.
위 그래프에선 x1과 x2가 상관관계를 지니기 때문에 많은 셀들이 비어있습니다. 이를 위해 가까운 비어있지 않은 셀들의 ALE 추정치로 비어있는 셀의 ALE 추정치를 대체할 수 있습니다.
다시 한 번 강조하지만 2차 효과란 특성값들의 주효과를 고려한 후의 추가적인 상호작용 효과를 나타냅니다. 2가지 특성이 상호작용하지 않지만 각각 예측 결과에 선형 관계를 지닌다고 가정해봅시다. 각 특성에 대해 1D ALE Plot은 직선이 그려질 것입니다. 반면, 상호작용 추가 효과만 나타내는 2D ALE Plot에선 0에 가까워질 것입니다. ALE Plot과 PDP는 여기서 다른 모습을 보입니다.
PDP는 항상 전체 효과를 보여주지만, ALE Plot은 1차(=주) 혹은 2차 효과를 나타내기 때문입니다. 이는 기초 수학에 의존하지 않는 설계 결정(design decision)입니다. PDP에서 낮은 차원의 효과를 빼서 주효과 혹은 2차 효과를 나타낼 수도 있고, 저차원 효과 감소를 제약하여 전체 ALE Plot의 추정치를 얻을 수도 있습니다.
카테고리 특성에 대한 ALE
정의상 ALE는 특정 방향으로 효과를 누적하기 때문에 특성값이 순서(order)를 가질 필요가 있습니다. 카테고리 특성값은 자연적인 순서가 없으므로 ALE Plot을 계산하려면 어떻게든 순서를 만들거나 찾아야 합니다.
해결 방법 중 하나는 다른 특성들을 토대로 유사성에 따라 정렬하는 것입니다. 2개 카테고리 사이의 거리는 각 특성 간 거리를 합한 것입니다. 특성 간 거리는 수치형 특성의 경우 2개 특성의 누적 분포(Kolmogorov-Smirmov 거리라고도 부름)를 비교하거나, 카테고리 특성의 경우 상대적 빈도 테이블을 비교합니다. 일단 모든 카테고리 간의 거리를 구하면 다차원 스케일링을 통해 거리 메트릭스를 1차원 거리 측도로 줄입니다. 이는 카테고리의 유사성에 기반한 순서를 제공해줍니다.
예를 들어 "계절"과 "날씨"라는 2가지 카테고리 특성과 수치형 특성인 "온도"를 가지고 있다고 가정합시다. 첫 번째 카테고리 특성값(계절)에 대해 ALE를 구하려고 합니다. 해당 특성은 "봄", "여름", "가을", "겨울"이란 카테고리가 있으며 먼저, "봄"과 "여름" 간의 거리를 계산해보겠습니다. 이는 "온도"와 "날씨" 특성값 간의 거리를 모두 합한 것입니다. 온도(수치형)에 대해 계절 "봄"에 해당하는 모든 인스턴스들을 가지고 경험적 누적 분포 함수(empirical cumulative distribution)를 계산하고, 계절 "여름"에 대해서도 동일하게 진행합니다. 그리고 Kolmogorov-Smirnov 통계를 통해 거리를 측정합니다.
날씨(카테고리)의 경우 모든 날씨 유형에 대한 확률을 "봄"에 해당하는 인스턴스에 대해 계산하고, "여름"에 해당하는 인스턴스도 마찬가지로 계산한 후 확률 분포의 절대적인 거리를 합산합니다. 만약 "봄"과 "여름"이 매우 다른 온도와 날씨를 보인다면 전체 카테고리 거리값은 클 것입니다. 이런 과정을 다른 날씨 쌍(pair)에 대해서도 진행하고 다차원 스케일링을 통해 최종 거리 메트릭스를 1차원으로 축소합니다.
예제
아래 예제에선 예측 모델과 2개의 강력한 상관관계를 가진 특성으로 구성되어 있습니다. 예측 모델은 대부분 선형 회귀 모델이지만, 인스턴스가 발견되지 않는 2가지 특성값의 조합에서 이상한 패턴을 보입니다.

음영 배경이 모델이 예측하는 값을 나타냅니다. x1이 0.7보다 크고 x2가 0.3보다 작을 경우 모델은 항상 값 2를 예측하는데, 해당 영역은 데이터 분포로부터 거리도 멀고 모델 성능에 영향을 주지도 않으며, 해석에도 영향을 미쳐서는 안됩니다.
모델은 학습할 때 기존 학습 데이터 인스턴스에 대해서만 손실을 최소화합니다. 따라서 학습 데이터 분포 밖에서 이상한 일이 일어날 가능성이 항상 존재합니다. 데이터 분포를 벗어나는 것을 보외법(extrapolation)이라고 하는데, 이는 적대적 예제 챕터에 설명되어 있는 머신러닝 모델을 속이는 데도 사용될 수 있습니다. ALE Plot과 비교하여 PDP가 어떻게 동작하는지 아래 예제를 참조하기 바랍니다.
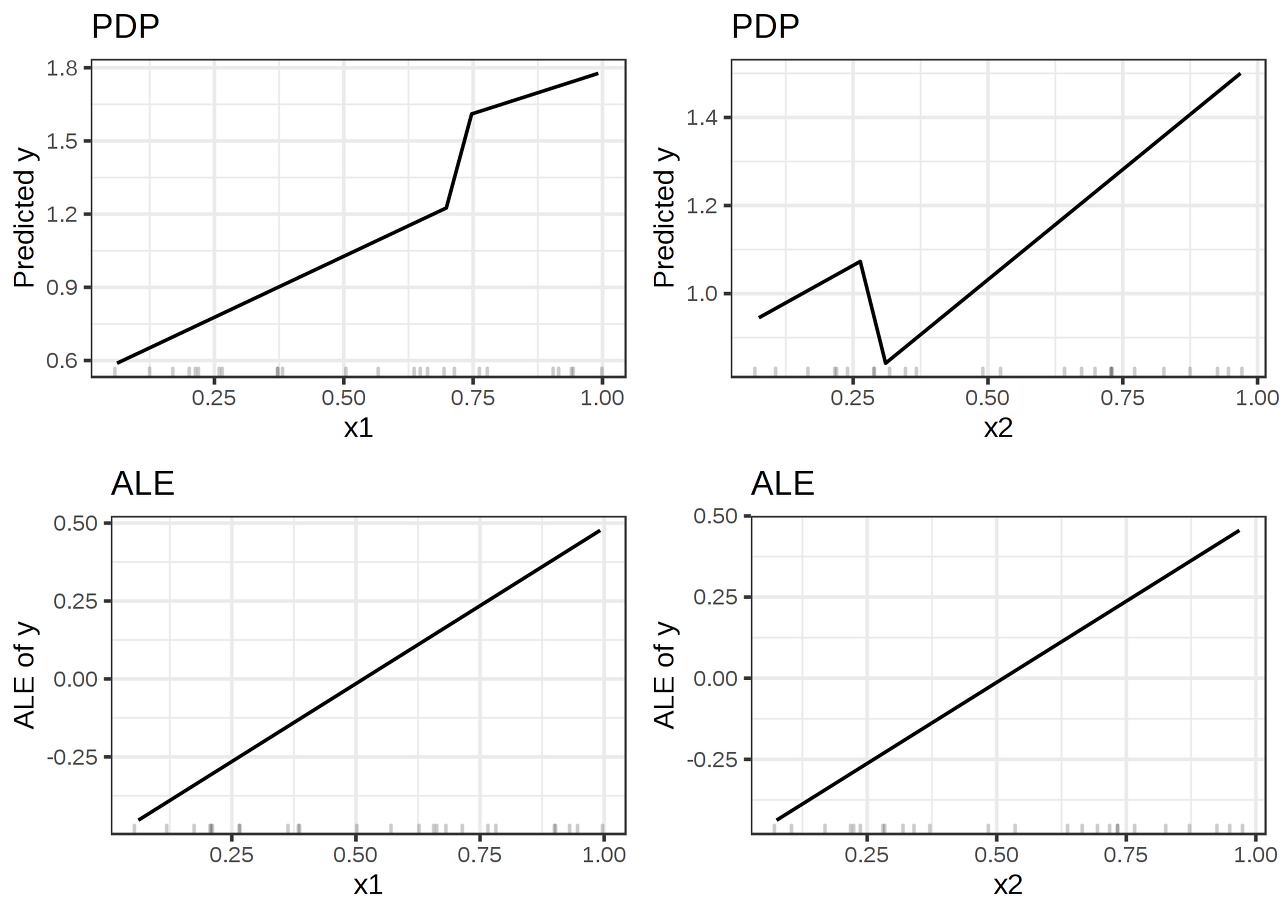
PDP 추정치는 데이터 분포 바깥에서 모델의 이상한 행동에 영향을 받습니다. 반면, ALE Plot은 데이터가 없는 영역은 무시한 채 특성과 예측 간의 선형 관계를 정확하게 파악했습니다.
날씨와 날짜를 기준으로 대여된 자전거 수를 예측하는 데이터셋을 보며 ALE Plot이 실제로 잘 작동하는지 확인해 봅시다. 특정한 날에 대여되는 자전거 수를 예측하는 회귀 모델을 학습하고, 온도, 상대 습도, 풍속이 예측에 어떤 영향을 미치는지 분석하기 위해 ALE Plot을 사용했습니다.
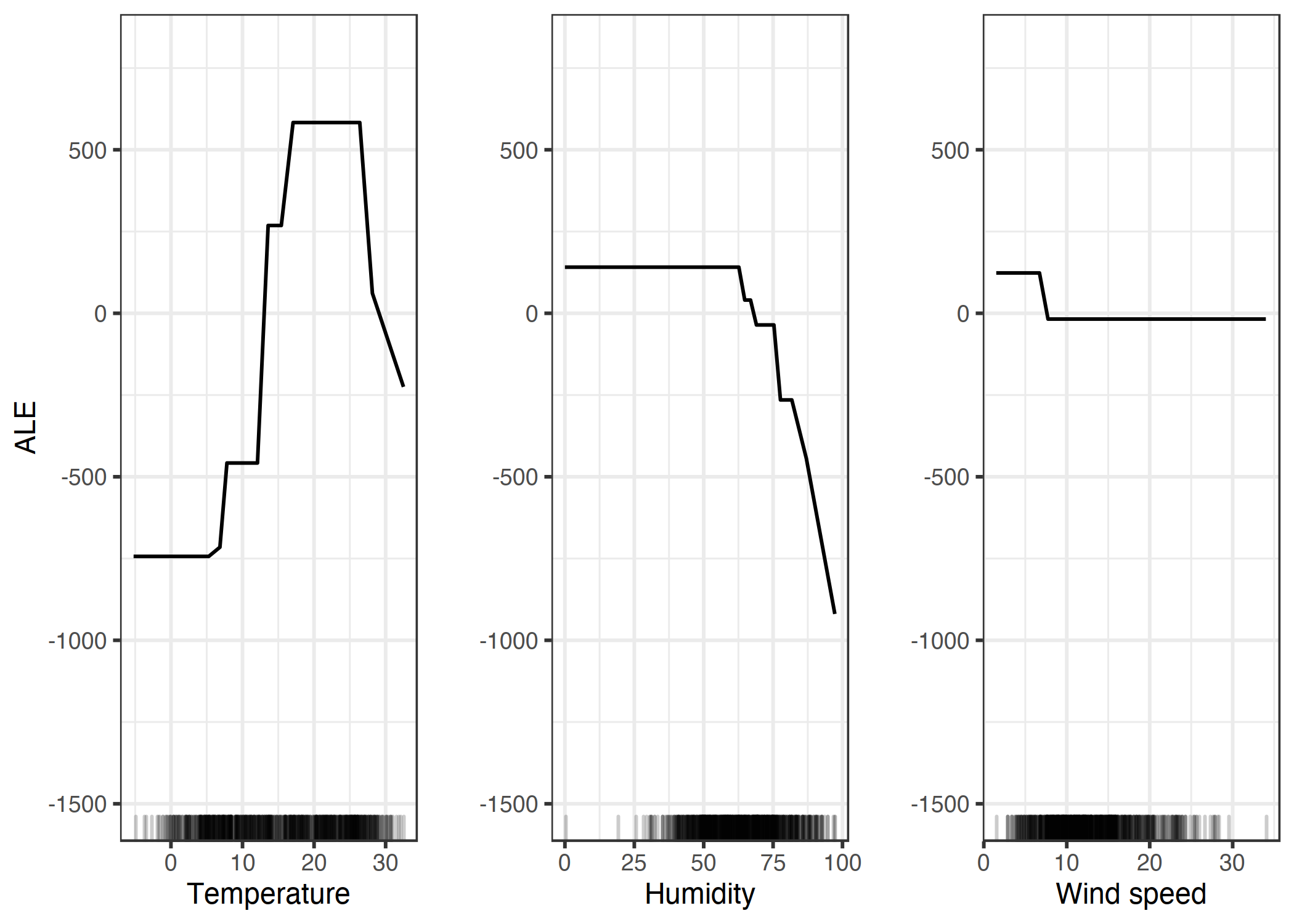
기온이 예측에 강한 영향을 미치며, 섭씨 25까지는 기온이 올라가면 예측이 올라가지만 그 이상부터는 떨어집니다. 습도는 부정적인 영향을 미치며, 60% 이상이면 습도가 높을수록 예측치가 낮아집니다. 풍속은 큰 영향을 주지 않습니다.
기온, 습도, 풍속과 다른 모든 특성들 간의 상관관계를 살펴봅시다. 카테고리 특성도 포함되어 있기 때문에 2개의 특성값이 모두 숫자일 때 작동하는 피어슨(Pearson) 상관계수를 사용할 수 없습니다. 대신 예를 들어 다른 특성들 중 하나를 입력으로 하여 온도를 예측하는 회귀 모델을 학습했다고 하죠. 그리고 선형 회귀 모델의 다른 특성이 분산을 얼마나 설명하는지를 측정하고 제곱근을 취합니다. 다른 특성이 수치형이라면, 결과는 피어슨 상관계수의 절댓값과 동일할 것입니다. 하지만 이런 모델 기반의 "variance-explained"(ANOVA라고도 불림, ANalysis Of VAriance) 접근법은 특성이 카테고리일 때도 작동합니다. "variance-explained" 측정은 항상 0(연관 없음)과 1(다른 특성으로부터 온도를 완벽하게 예측) 사이의 값을 가집니다. 이렇게 온도, 습도, 풍속의 설명된 분산을 다른 모든 특성들과 함께 계산합니다. 설명된 분산이 높을수록 PDP에서 더 많은 문제가 발생할 수 있습니다.
아래는 날씨 특성이 다른 특성들과 얼마나 강하게 연관되어 있는지를 시각화한 것입니다.
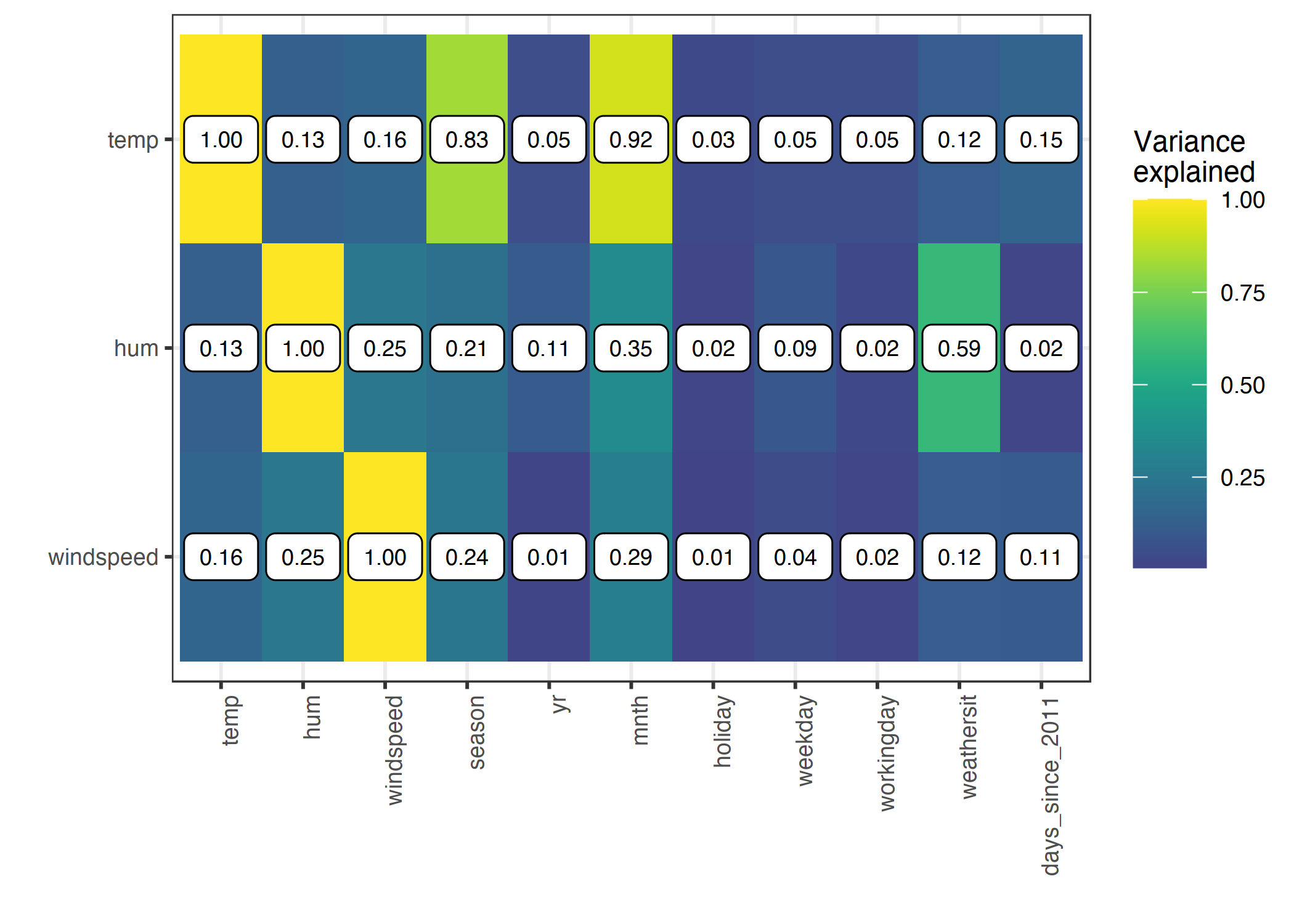
온도, 습도, 풍속과 모든 특성 간의 상관관계는 설명된 분산 양으로 측정됩니다. 온도 특성의 경우, 계절(season) 및 월(month)과 높은 상관관계를 보이고 있습니다. 습도는 기상 상황(weather situation)과 관련이 있는 듯합니다.
이러한 상관관계 분석은 PDP, 특히 온도 특성과 관련하여 문제에 직면할 수 있음을 보여줍니다.
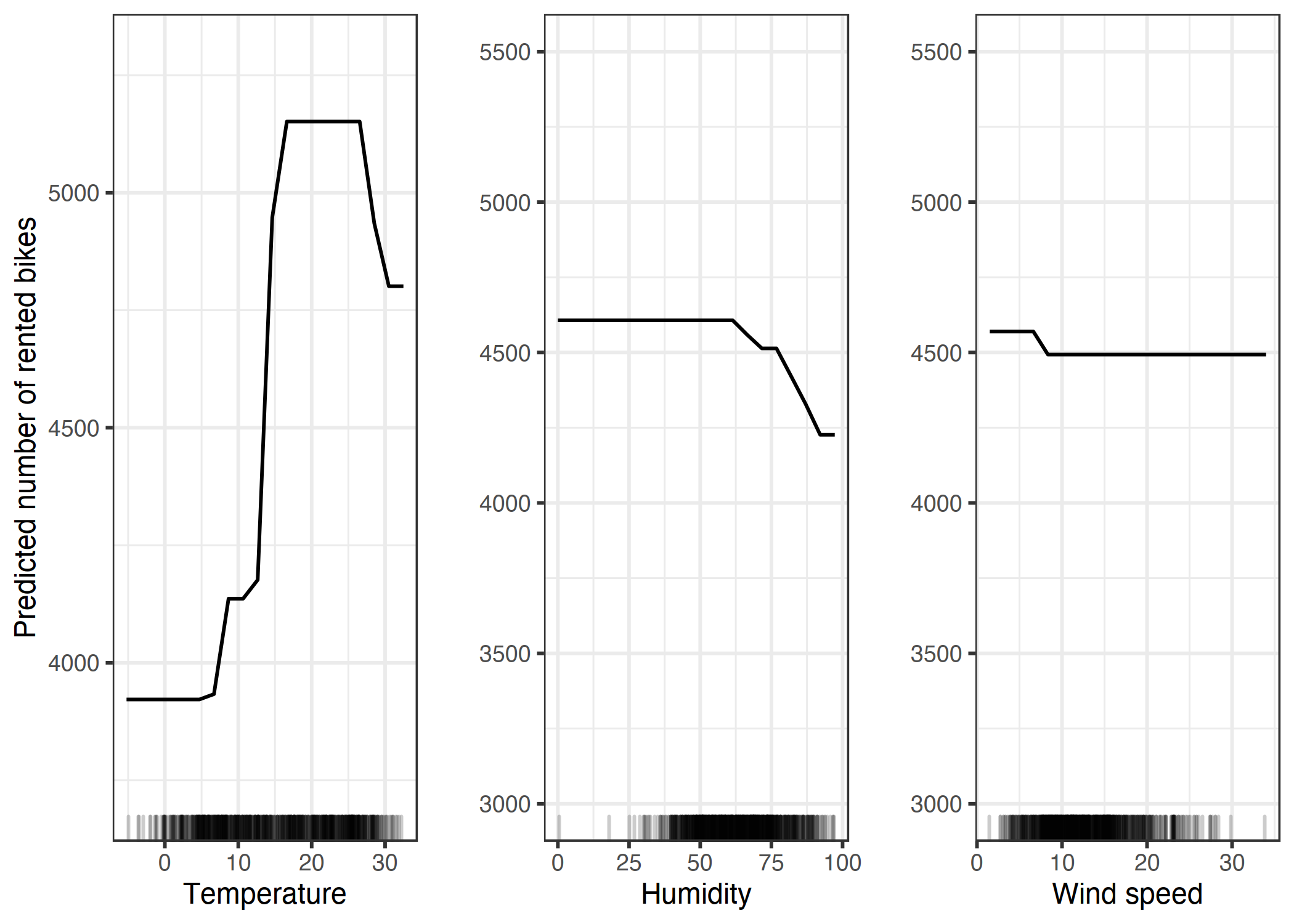
ALE Plot에 비해 PDP는 높은 온도나 습도에 대한 예상 자전거 수가 더 적게 감소했음을 보여줍니다. PDP는 계절이 "겨울"이라 하더라도 모든 데이터 인스턴스를 사용하기 때문에 고온의 영향을 계산합니다.
이제 카테고리 특성에 대한 ALE Plot을 보고자 합니다. 각 월은 모델이 예측한 자전거 수에 대한 효과를 분석하고자 하는 카테고리 특성에 해당합니다. 논쟁의 여지가 있지만, 각 월은 이미 일정한 순서(1월 ~ 12월)를 가지고 있습니다. 일단 유사성에 의해 카테고리를 재정렬하고 그 결과를 계산합니다. 온도나 휴일 여부와 같은 다른 특성에 근거하여 각 월의 날짜(day) 유사성을 구하고 이에 따라 각 월이 정렬됩니다.
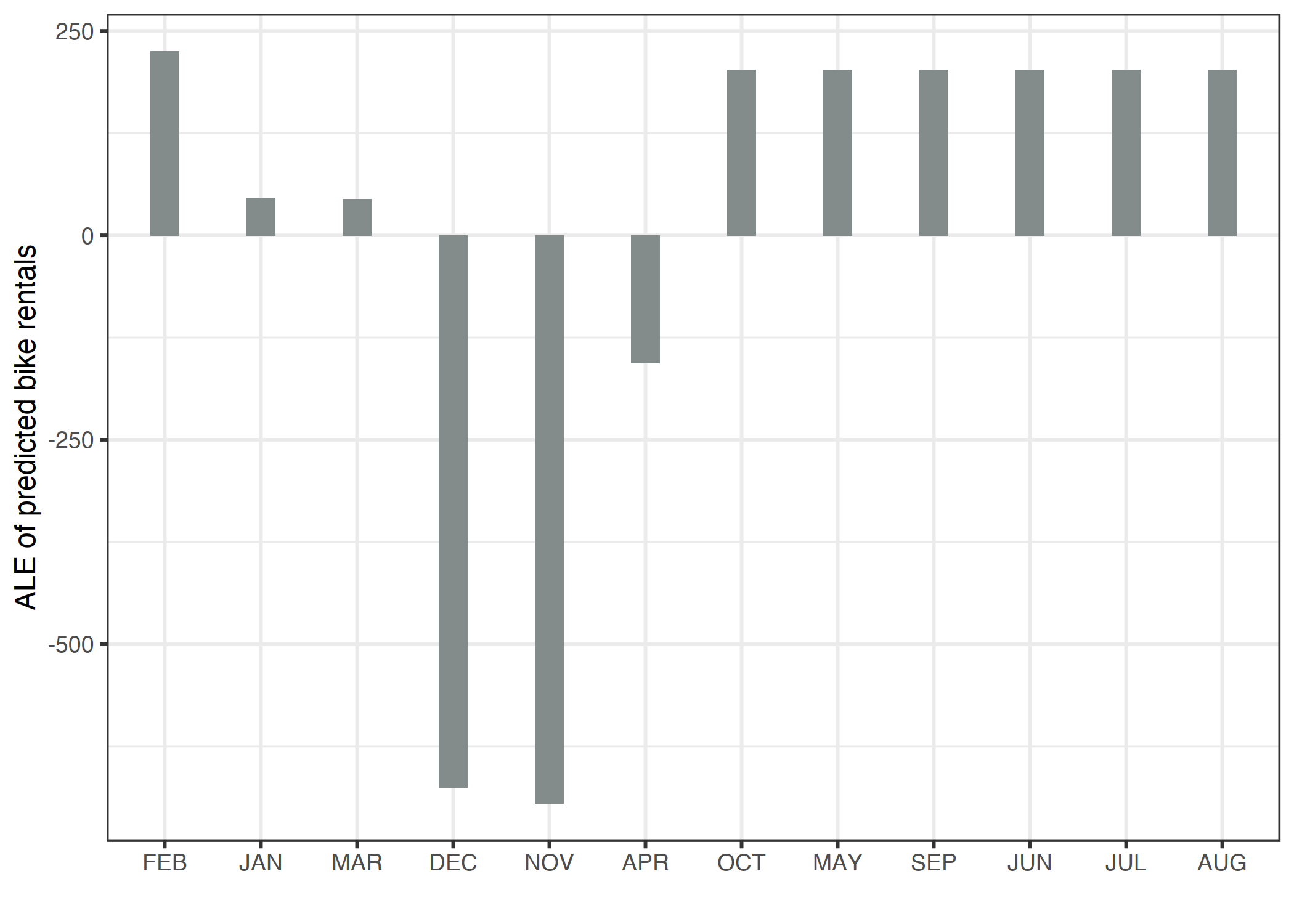
월별 다른 특성값의 분포에 기초하여 서로 간의 유사성에 따라 각 월이 정렬됩니다. 1월, 3월, 4월 특히 11월, 12월은 예상 자전거 수에 대한 효과가 낮다는 것을 알 수 있습니다.
많은 특성들이 날씨와 관련되어 있기 때문에, 월 순서는 각 월 간 날씨가 얼마나 비슷한지를 강하게 반영합니다. 더 추운 달은 모두 왼쪽(2월 ~ 4월)에 위치하고, 따뜻한 달은 오른쪽(10월 ~ 8월)에 위치합니다. 하지만 날씨와 관련 없는 휴일과 같은 특성 역시 유사성 계산에 포함되어 있음을 유념해야 합니다.
다음으로 습도와 온도의 2차 효과를 살펴보도록 합니다. 2차 효과는 2개 특성값의 추가 상호작용 효과로 주효과를 포함하지 않는다는 사실을 기억해야 합니다. 다시 말하면, 2차 ALE Plot에서 높은 습도로 인해 평균적으로 예상 자전거 수가 감소하는 주효과를 보지 못한다는 것입니다.
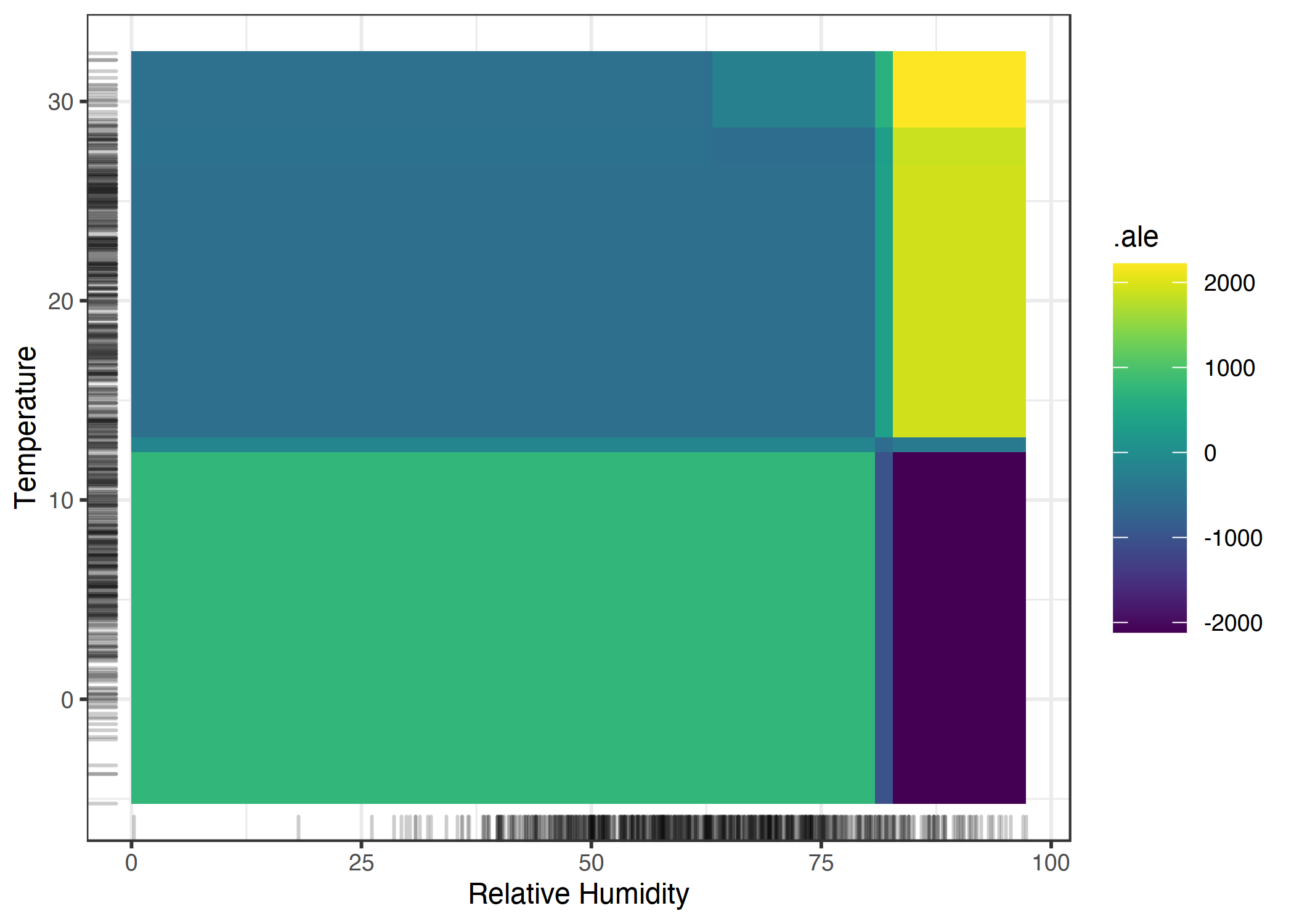
온도와 습도 간의 상호작용을 나타냅니다. 덥고 습한 날씨는 예상 자전거 수를 증가시키고, 춥고 습한 날씨는 감소시키는 모습이 보입니다.
온도와 습도 각각의 주효과는 더울수록, 습할수록 예상 자전거 수가 감소한다는 것을 명심해야 합니다. 덥고 습한 날씨는 온도와 습도의 결합 효과가 주효과의 합이 아니라 그 합보다 커집니다. 순수 2차 효과와 총 효과 간의 차이를 강조하기 위해, PDP를 함께 살펴봅시다. PDP는 평균 예측, 2개의 주효과 및 2차 효과를 합친 총 효과를 나타냅니다.
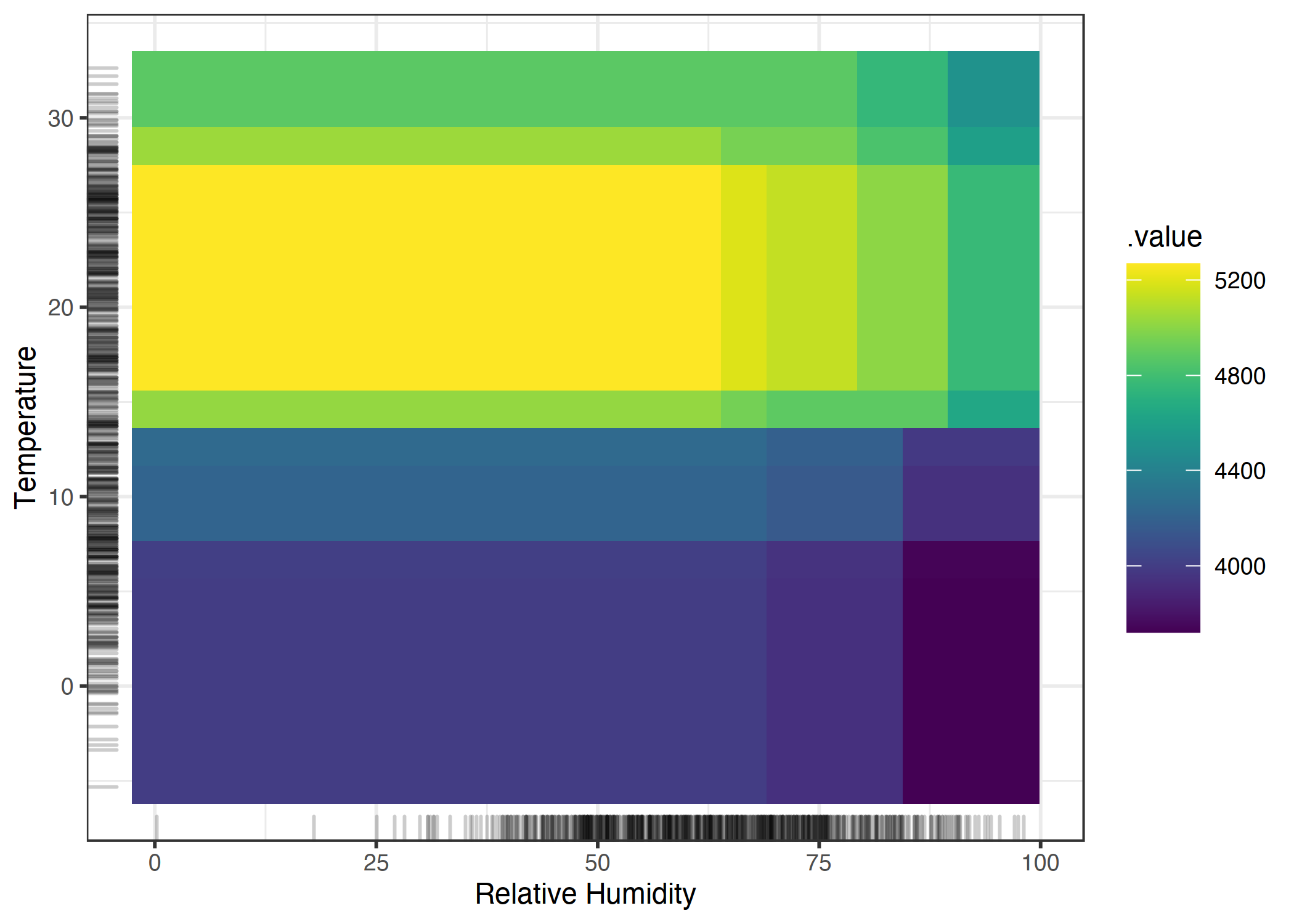
위의 PDP는 각 특성의 주효과와 그들 간의 상호작용 효과를 결합한 형태를 보여줍니다.
이제 자궁경부암 발생 가능성을 예측하는 분류 작업을 살펴보도록 합니다. 랜덤포레스트로 모델을 학습시키고 2가지 특성에 대한 누적 지역 효과를 시각화합니다.
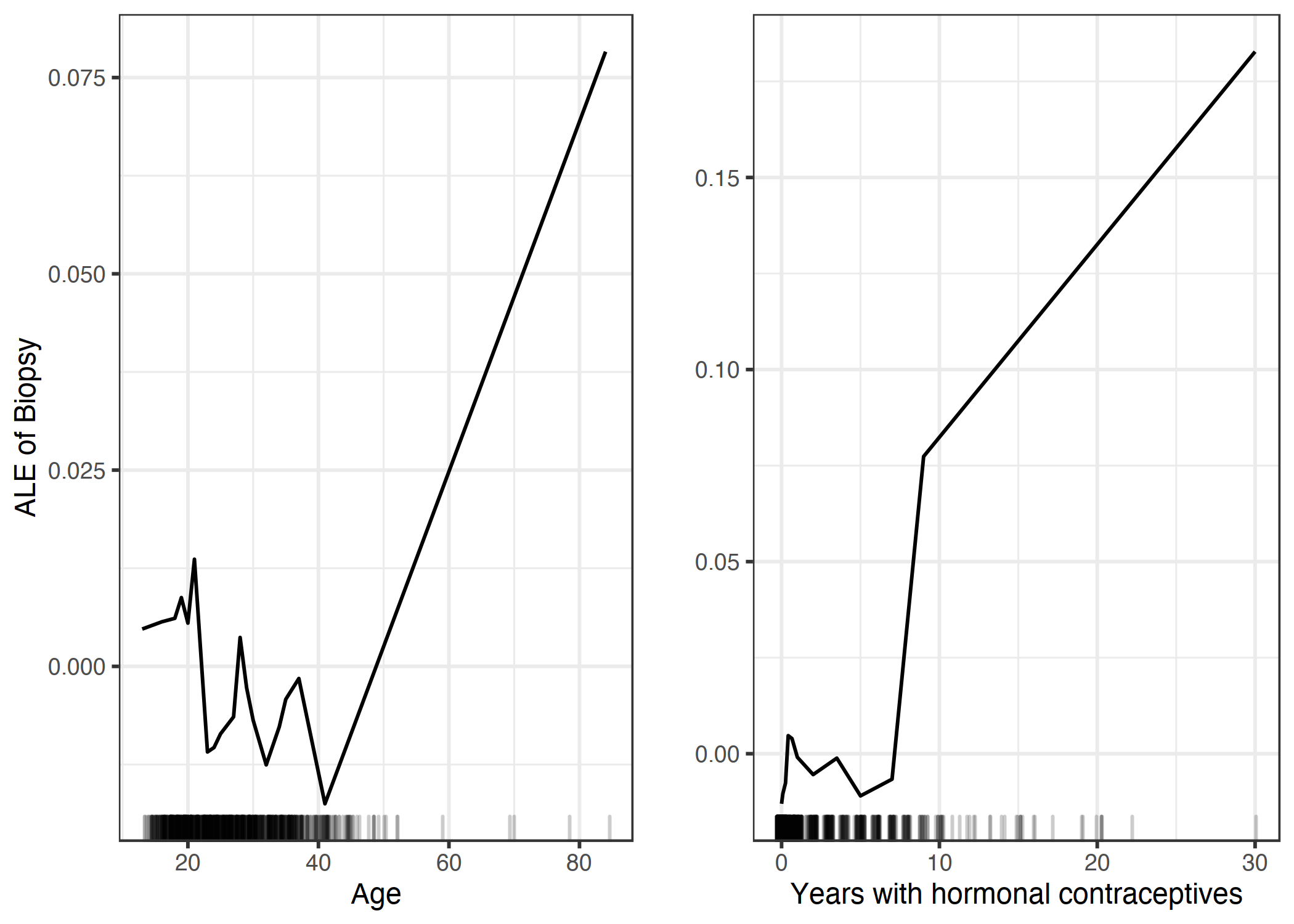
나이와 호르몬 피임약을 복용한 나이가 자궁경부암 예측 확률에 미치는 영향을 나타냅니다. 나이 특성의 경우 평균 40세까지 낮으며 그 이후 증가하는 모습을, 호르몬 피임약 복용 나이의 경우 8년 후 발생 위험이 더 높아짐을 보입니다.
아래는 임신 횟수와 나이 사이의 상호작용을 나타내는 그래프입니다.
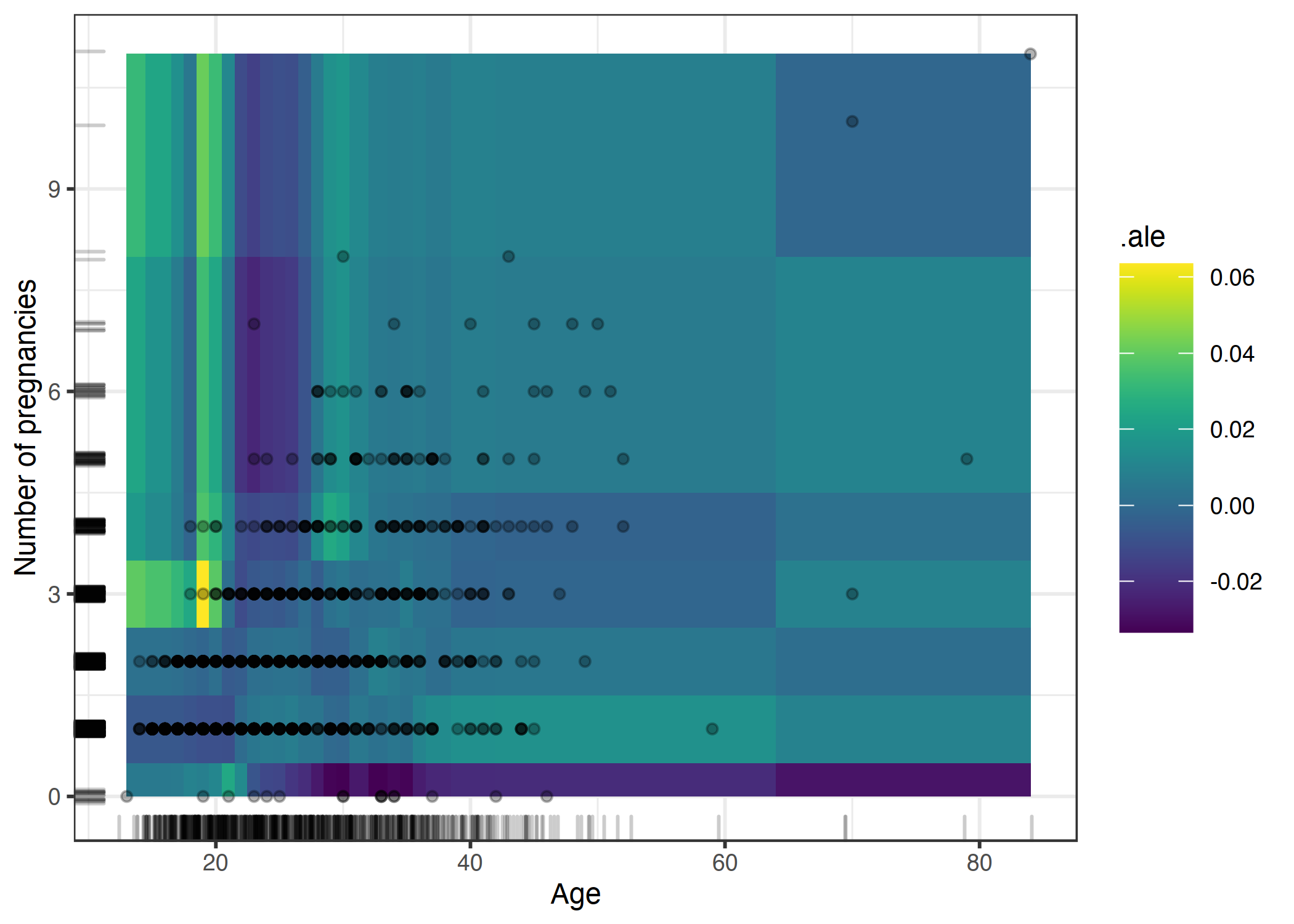
위 그래프 해석은 깔끔하지 않는데, 18~20세 및 3회 이상의 임신에서 암 발생 확률이 최대 5% 포인트 증가합니다. 해당 나이에 임신 횟수를 가진 여성은 실제로 많지 않기 때문에 모델이 관련 영역에서 이상한 행동을 보여도 학습 과정에서 패널티를 받지 않습니다.
장점
1. ALE Plot은 편향이 없으며, 이는 특성 간 상관관계에도 여전히 작용함을 의미합니다.
2. PDP보다 계산 속도가 빠르며 시간 복잡도는 O(n)입니다. PDP는 그리드 값 추정치의 n배를 요구합니다.
3. 해석이 명확하여, 특성값의 변경이 예측에 미치는 상대적 효과를 읽을 수 있습니다.
단점
1. 구간 수가 많아 약간 불안정할 수 있습니다. 구간 수를 줄이면 추정치가 더 안정적이게 되고 예측 모형의 실제 복잡성을 완화하거나 숨길 수 있습니다. 구간 수를 설정하기 위한 완벽한 해결책은 없습니다. 숫자가 너무 작으면 ALE Plot이 그다지 정확하지 않거나, 너무 많으면 곡선이 흔들릴 수 있습니다.
2. PDP와 달리 ICE 곡선이 동반되지 않습니다. ICE 곡선은 특성값 효과에서 이질성을 드러낼 수 있고, 이는 데이터 하위 집합에 대해 특성값 효과가 다르게 보일 수 있음을 의미합니다. ALE Plot의 경우 인스턴스 간에 효과가 다른지 여부를 구간별로만 확인 가능하고, 각 구간마다 인스턴스가 다르기 때문에 ICE 곡선과 같지 않습니다.
3. 2차 ALE 추정치는 특성 공간(feature space) 전체에 걸쳐 변화 안정성(varying stability)을 가지며, 이는 어떤 방식으로도 시각화되지 않습니다. 그 이유는 셀에서 지역적 효과의 각 추정치가 다른 수의 데이터 인스턴스를 사용하기 때문입니다. 결과적으로, 모든 추정은 다른 정확도를 가지고 있습니다(하지만 여전히 가능한 최선의 추정치임).
이 문제는 주효과 ALE Plot에선 덜 심각하게 나타납니다. 사분위수를 격자로 사용한 덕분에 모든 구간에서 인스턴스 수는 동일하지만, 일부 영역에서는 짧은 구간이 많을 것이며 ALE 곡선은 더 많은 추정치로 구성될 것입니다. 하지만 전체 곡선의 큰 부분을 차지하는 긴 구간의 경우, 상대적으로 적은 수의 인스턴스가 존재할 것입니다.
4. 2차 효과 플롯은 주효과를 항상 염두에 두어야 하기 때문에 해석하기가 좀 귀찮아질 수 있습니다. 적외선 열지도를 두 특성값의 전체 효과로 받아들이는 것은 유혹적이지만, 이는 상호작용의 부가적인 효과일 뿐입니다. 순수한 2차 효과는 상호작용을 발견하고 탐구하는 데 흥미롭지만, 그 효과가 어떻게 나타나는지를 해석하는 데는 주효과를 플롯에 통합하는 것이 더 합리적입니다.
5. ALE Plot이 편향이 없다 하더라도 특성 간 강한 상관관계가 있을 경우 해석은 여전히 어렵습니다. 해당 내용은 ALE Plot 뿐만 아니라 강한 상관관계를 가진 특성들의 일반적인 문제입니다.
이번 챕터 내용에 따르면 경험적으로 PDP 보단 ALE Plot을 사용하는 것이 낫다고 합니다 :)
참조
https://christophm.github.io/interpretable-ml-book/ale.html
'문돌이 존버 > 데이터 분석' 카테고리의 다른 글
| (Explainable AI) Counterfactual Explanations (0) | 2021.09.16 |
|---|---|
| (Explainable AI) 변수 상호작용 개념 이해하기 (0) | 2021.08.26 |
| 핸즈온 머신러닝 2 복습하기(챕터10: 케라스를 사용한 인공 신경망 소개) (0) | 2021.08.19 |
| (Explainable AI) Individual Condition Expectation 개념 이해하기 (0) | 2021.08.17 |
| 시퀀스-투-시퀀스(sequence-to-sequence) 간단히 이해하기 (0) | 2021.08.16 |



