본 글에는 생물학적 뉴런에서 인공 뉴런까지의 소카테고리인 10.1.1 생물학적 뉴런, 10.1.2 뉴런을 사용한 논리 연산은 제외한다.
다만, 짚고 넘어갈 내용은 인공 신경망에서 활성화 함수(=비선형 함수)를 사용한다는 것이다. 딥러닝 탄생 자체가 세상의 여러 (비선형적) 문제를 해결하기 위함으로 은닉층을 거친 선형 함수(w1x1+w2x2+...wnxb+bw1x1+w2x2+...wnxb+b)를 비선형화하는 것이 필요하다. 활성화 함수로 선형 함수를 쓰면 은닉층을 몇 번 쌓아도 결국 선형 함수가 만들어지게 된다.
활성화 함수는 본래 다음 은닉층에 신호를 전달할 것인지를 판단하는 역할을 수행하면서 특정 임곗값(threshold)을 넘은 뉴런의 신호만 전달한다(activate). 예를 들어, 활성화 함수 중 하나인 시그모이드(sigmoid) 함수의 경우 임곗값 0.5 이상이면 1을, 이하면 0을 리턴하여 신호 전달 여부를 결정한다.
나중에 살펴볼 역전파(backpropogation) 계산을 위해서도 비선형 함수가 필요하다. 선형 함수는 도함수가 상수값이기 때문에 근본적으로 학습이 불가능하기 때문이다.
10. 케라스를 사용한 인공 신경망 소개
10.1.3 퍼셉트론
퍼셉트론(perceptron)은 TLU(threshold logic unit) 또는 이따금 LTU(linear threshold unit)라고 불리는 조금 다른 형태의 인공 뉴런을 기반으로 한다. TLU는 입력의 가중치 합을 계산(z=w1x1+w2x2+...+wnxn=xTw)한 뒤 계산된 합에 계단 함수(step function)를 적용하여 결과를 출력한다.
hw(x)=step(z), 여기에서 z=xTw

퍼셉트론에서 가장 널리 사용되는 계단 함수는 헤비사이드 계단 함수(Heaviside step function)이다.
heaviside(z)=0, z<0일때/1, z≥0일때
sgn(z)=−1, z<0일때/0, z=0일때/+1, z>0일때
퍼셉트론은 층이 하나뿐인 TLU로 구성되며, 각 TLU는 모든 입력에 연결되어 있다. 한 층에 있는 모든 뉴런이 이전 층의 모든 뉴런과 연결되어 있을 때, 이를 완전 연결 층(fully connected layer) 또는 밀집 층(dense layer)라고 한다.

입력층에 보통 편향 특성이 더해지며, 이는 항상 1을 출력하는 특별한 종류의 편향 뉴런(bias neuron)으로 표현된다.
선형대수학을 통해 한 번에 여러 샘플에 대해 인공 뉴런 층의 출력을 효율적으로 계산하는 식은 아래와 같다.
hw,b(X)=ϕ(XW+b)
X: 입력 특성 행렬(행 -> 샘플, 열 -> 특성)
W: 가중치 행렬(행 -> 입력 뉴런, 열 -> 출력층 인공 뉴런)
편향 뉴런을 제외한 모든 연결 가중치 포함
ϕ: 활성화 함수(activation function)
퍼셉트론에 한 번에 한 개의 샘플이 주입되면 각 샘플에 대해 예측이 만들어진다. 잘못된 예측을 하는 모든 출력 뉴런에 대해 올바른 예측을 만들 수 있도록 입력에 연결된 가중치를 강화시킨다. 가중치를 업데이트하는 수식은 아래와 같다.
w(nextstep)i,j=wi,j+η(yi−ˆyj)xi
wi,j: i번째 입력 뉴런과 j번째 출력 뉴런 사이를 연결하는 가중치
xi: 현재 훈련 샘플의 i번째 뉴런의 입력값
ˆyj: 현재 훈련 샘플의 j번째 출력 뉴런의 출력값
yj: 현재 훈련 샘플의 j번째 출력 뉴런의 타깃값
η: 학습률
각 출력 뉴런의 결정 경계는 선형이므로 퍼셉트론 역시 복잡한 패턴을 학습하지는 못한다. 하지만 로젠블라트는 훈련 샘플이 선형적으로 구분될 수 있다면 이 알고리즘이 정답에 수렴한다는 것을 증명했다. 이를 퍼셉트론 수렴 이론(perceptron convergence theorem)이라고 한다.
사이킷런은 하나의 TLU 네트워크를 구현한 Perceptron 클래스를 제공한다.
import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import Perceptron
iris = load_iris()
X = iris.data[:, (2, 3)] # 꽃잎 길이와 너비
y = (iris.target == 0).astype(np.int) # Iris Setosa인지?
per_clf = Perceptron()
per_clf.fit(X, y)
y_pred = per_clf.predict([[2, 0.5]])
print(y_pred) # [0]퍼셉트론을 여러 개 쌓아올리면 일부 제약을 줄일 수 있는데, 이런 인공 신경망을 다층 퍼셉트론(Multi-layer perceptron, 이하 MLP)이라 한다. MLP는 XOR 문제를 풀 수 있는데 아래 그림을 참고하자. 입력이 (0, 0)이나 (1, 1)일 때 네트워크가 0을 출력하고, 입력이 (0, 1)이나 (1, 0)일 때 1을 출력한다.
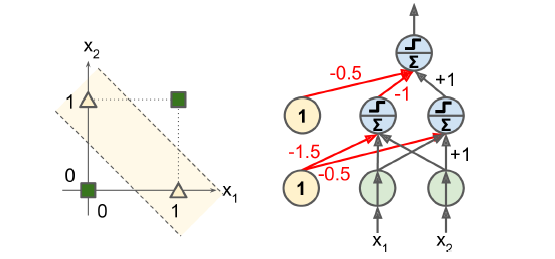
10.1.4 다층 퍼셉트론과 역전파
MLP는 입력층(input layer) 하나와 은닉층(hidden layer) 하나 이상의 TLU 층과 마지막 출력층(output layer)으로 구성된다.
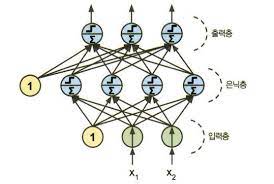
위 MLP 경우 신호가 입력에서 출력으로 한 방향으로만 흐르며, 이런 구조는 피드포워드 신경망(feedforward neural network)에 속한다.
은닉층을 여러 개 쌓아 올린 인공 신경망을 심층 신경망(deep neural network, 이하 DNN)이라 한다. MLP를 훈련하는 방법은 역전파(backpropogation) 알고리즘을 사용한다. 참고로 이는 1986년 데이비드 루멜하트, 제프리 힌턴, 로날드 윌리엄스가 논문1에서 공개한 것이다.
역전파 작동은 사실 앤드류 응의 강의를 참고하는 것이 가장 좋다. 여기선 로직만 간단하게 살펴보고 넘어가며, 수식은 없다.
1. 한 번에 하나의 미니배치씩 진행하여 전체 훈련 세트를 처리한다. 이 과정을 여러 번 반복하는데 각 반복을 에포크(epoch)라 부른다.
2. 각 미니배치는 네트워크의 입력층으로 전달되어 첫 번째 은닉층으로 보내진다. 그다음 (미니배치에 있는 모든 샘플에 대해) 해당 층에 있는 모든 뉴런의 출력을 계산한다.
-> 이 결과는 다음 층으로 전달된다. 다시 이 층의 출력을 계산하고 결과는 다음 층으로 전달된다. 이것이 정방향 계산(forward pass)이다.
3. 알고리즘이 네트워크의 출력 오차를 측정한다.
4. 각 출력 연결이 이 오차에 기여하는 정도를 계산한다. 미적분에서 기본 규칙이 되는 연쇄 법칙(chain rule)을 적용하면 빠르고 정확하게 수행할 수 있다.
-> 입력층에 도달할 때까지 역방향으로 계속된다.
5. 경사 하강법을 수행하여 방금 계산한 오차 그레이디언트를 사용해 네트워크에 있는 모든 연결 가중치를 수정한다.
은닉층의 연결 가중치를 랜덤하게 초기화하는 것이 중요하다. 예를 들어 가중치와 편향을 모두 0으로 초기화하면 층의 모든 뉴런이 완전히 같아지므로 훈련의 의의가 없다.
논문의 저자들은 역전파 알고리즘을 더 업그레이드하기 위해 계단 함수를 로지스틱(시그모이드) 함수로 바꿨다.
σ(z)=1/(1+exp(−z))
로지스틱 함수는 어디서든지 0이 아닌 그레이디언트가 잘 정의되어 있다. 이외에도 널리 쓰이는 두 개의 활성화 함수는 아래와 같다.
1. 하이퍼볼릭 탄젠트 함수
tanh(z)=2σ(2z)−1
훈련 초기에 각 층의 출력을 원점 근처로 모으는 경향이 있어 종종 빠르게 수렴되도록 도움
2. ReLU 함수
ReLU(z)=max(0,z)
z=0에서 미분 가능하지 않아 기울기가 갑자기 변해 경사 하강법이 엉뚱한 곳으로 튈 수 있다. 실제로 잘 작동하고 계산 속도가 빠르다는 장점이 있다. 무엇보다 중요한 점은 출력에 최댓값이 없다는 점이 경사 하강법에 있는 일부 문제(local minimum)를 완화해준다.
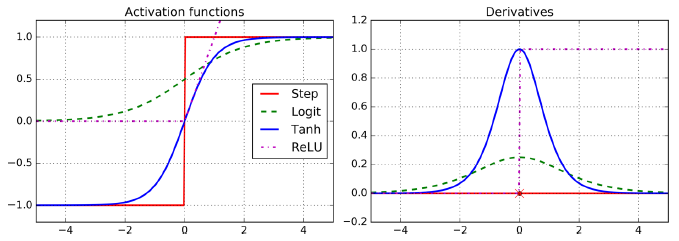
이처럼 비선형 활성화 함수가 있는 충분히 큰 DNN은 이론적으로 어떤 연속 함수(continuous function)도 근사할 수 있다.
10.1.5. 회귀를 위한 다층 퍼셉트론
일반적으로 회귀용 MLP를 만들 때 출력 뉴런에 활성화 함수를 사용하지 않고 어떤 범위의 값도 출력되도록 한다. 하지만 출력이 항상 양수여야 한다면 출력층에 ReLU 활성화 함수를 사용할 수 있다. 어떤 범위 안의 값을 예측하고 싶다면 로지스틱 함수나 하이퍼볼릭 탄젠트 함수를 사용하고 레이블의 스케일을 적절한 범위를 조정할 수 있다.
훈련에 사용하는 손실 함수는 전형적으로 평균 제곱 오차(MSE)이다. 하지만 훈련 세트에 이상치가 많다면 평균 절댓값 오차(MAE)를 사용할 수 있다. 또는 이 둘을 조합한 후버(Huber) 손실을 사용할 수 있다.
후버 손실은 오차가 임곗값 δ(전형적으로 1)보다 작을 때 2차 함수다. 오차가 δ보다 클 때는 선형 함수다. 선형 함수 부분은 MSE보다 이상치에 덜 민감하다. 2차 함수 부분은 MAE보다 더 빠르고 정확하게 수렴하도록 한다.
10.1.6 분류를 위한 다층 퍼셉트론
이진(binary) 분류 문제에선 로지스틱 활성화 함수를 가진 하나의 출력 뉴런만 필요하다. 출력은 0과 1 사이의 실수이며, 이는 양성 클래스에 대한 예측 확률로 해석할 수 있다.
다중(multiclass) 분류 문제에선 출력층에서 소프트맥스 활성화 함수를 사용해야 한다. 소프트맥스 함수는 모든 예측 확률을 0과 1사이로 만들고 더했을 때 1이 되도록 만든다.
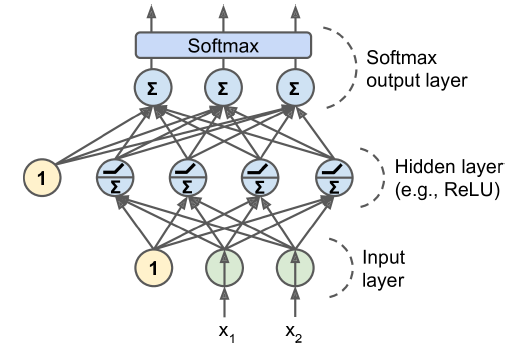
확률 분포를 예측해야 하므로 손실 함수에는 일반적으로 크로스 엔트로피 손실(cross-entropy loss)을 선택하는 것이 좋다.
# Sequential API 사용
model = keras.models.Sequential()
model.add(keras.layers.Flatten(input_shape=[28, 28]))
model.add(keras.layers.Dense(300, activation='relu'))
model.add(keras.layers.Dense(100, activation='relu'))
model.add(keras.layers.Dense(10, activation='softmax'))
# 혹은
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation='relu'),
keras.layers.Dense(100, activation='relu'),
keras.layers.Dense(10, activation='softmax')
])Sequential: 순서대로 연결된 층을 일렬로 쌓아 구성
Flatten: 입력 이미지를 1D 배열로 변환
입력 데이터 X를 받으면 X.reshape(-1, 1)를 계산하는 간단한 전처리를 수행
모델의 첫 번째 층으로 input_shape를 지정하는데, 배치 크기를 제외한 샘플의 크기만 써야 함
Dense: 층마다 각자 가중치 행렬을 관리
가중치 행렬에는 층의 뉴런과 입력 사이의 모든 연결 가중치가 포함
model.summary()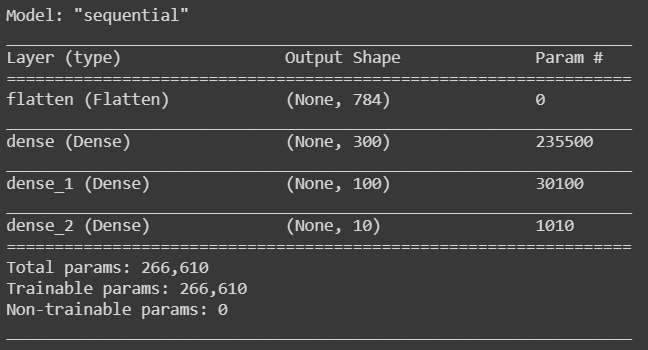
summary() 에 표시된 내용은 아래와 같습니다.
각 층 이름(지정하지 않으면 자동 생성, 지정은 names 매개변수 사용)
출력 크기(None은 배치 크기에 어떤 값도 가능하다는 의미)
파라미터 개수
모델에 있는 층의 리스트를 출력하거나 인덱스로 층을 쉽게 선택할 수 있다.
from pprint import pprint
pprint(model.layers)
hidden1 = model.layers[1]
print(hidden1.name)
print(model.get_layer('dense') is hidden1)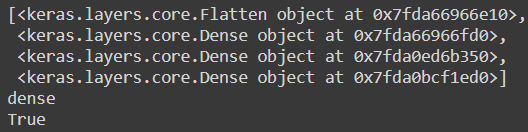
층의 모든 파라미터는 get_weights() 메서드와 set_weights() 메서드를 사용해 접근할 수 있다. Dense층의 경우 연결 가중치와 편향이 포함되어 있다.
weights, biases = hidden1.get_weights()
pprint(weights)
print(weights.shape)
print(biases)
print(biases.shape)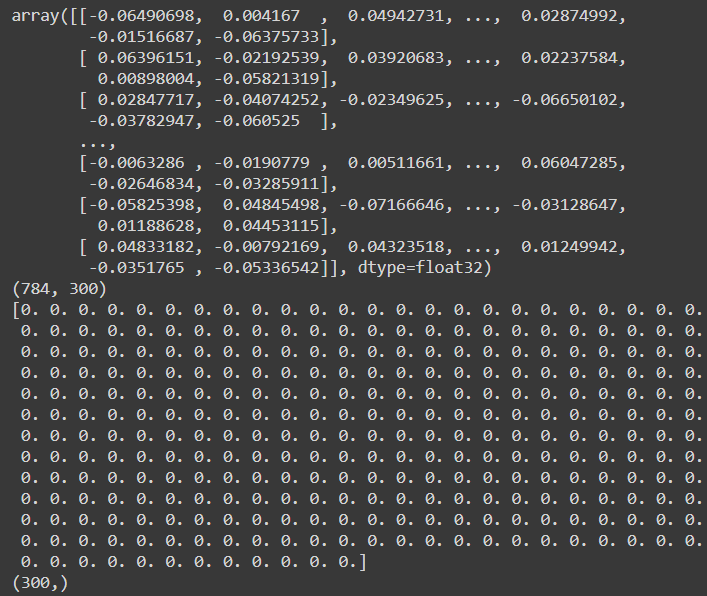
모델 컴파일
model.compile(loss='sparse_categorical_crossentropy',
optimizer='sgd',
metrics=['accuracy'])레이블이 정수 하나로 이루어져 있고(즉 샘플마다 타깃 클래스 인덱스 하나가 있음) 클래스가 배타적이므로 "sparse_categorical_crossentropy" 손실을 사용한다. 만약 샘플마다 클래스별 타깃 확률을 가지고 있다면(예를 들어 클래스 3의 경우 [0., 0., 0., 1., 0., 0., 0., 0., 0., 0.]인 one-hot 벡터라면) 대신 "categorical_crossentropy" 손실을 사용해야 한다.
이진 분류를 수행한다면 출력층에 "softmax" 함수 대신 "sigmoid" 함수를 사용하고 "binary_crossentropy" 손실을 사용한다.
참고
sparse label을 one-hot 벡터 레이블로 변환하려면 keras.utils.to_categorical() 함수를 사용한다. 그 반대로 변환하려면 axis=1로 지정하여 np.argmax() 함수를 사용한다.
옵티마이저 "sgd"는 기본 확률 경사 하강법(stocastic gradient descent)를 사용하여 모델을 훈련한다는 의미다. SGD 옵티마이저는 학습률(learning rate)을 튜닝하는 것이 중요한데, 기본값은 lr=0.01 을 사용한다.
모델 훈련과 평가
history = model.fit(X_train, y_train, epochs=30, validation_data=(X_valid, y_valid))
validation_data 매개변수에 검증에 사용할 훈련 세트의 비율을 지정할 수도 있다. validation_split=0.1 로 쓰면 검증에 (섞기 전) 데이터의 마지막 10%를 사용한다.
어떤 클래스는 많이 등장하고 다른 클래스는 조금 등장하여 편중된 상태라면 fit() 메서드를 호출할 때 class_weight 매개변수를 지정하는 것이 좋다. 적게 등장하는 클래스는 높은 가중치를 부여하고 많이 등장하는 클래스는 낮은 가중치를 부여한다. 샘플별로 가중치를 부여하고 싶다면 sample_weight 매개변수를 지정한다. (만약 둘 다 지정되면 케라스는 두 값을 곱하여 사용한다.)
fit() 메서드가 리턴하는 History 객체에는 1) 훈련 파라미터(history.params), 2) 수행된 에포크 리스트(history.epoch)가 포함된다. 가장 중요한 속성은 에포크가 끝날 때마다 훈련 세트와 (있다면) 검증 세트에 대한 손실과 측정한 지표를 담은 딕셔너리(history.history)다.
import pandas as pd
import matplotlib.pyplot as plt
pd.DataFrame(history.history).plot(figsize=(8, 5))
plt.grid(True)
plt.gca().set_ylim(0, 1) # 수직축 범위를 [0-1] 사이로 설정
plt.show()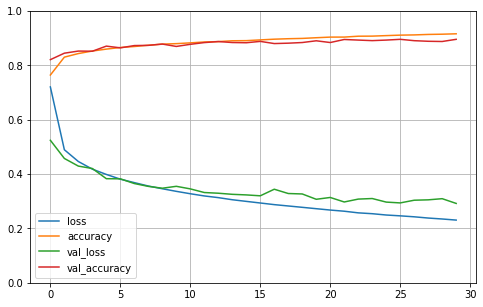
모델 성능이 만족스럽지 않으면 하이퍼파라미터를 튜닝해야 하는데, 1) 맨 처음 확인할 것은 학습률이다. 학습률이 도움이 되지 않는다면 2) 다른 옵티마이저를 테스트해야 한다. 항상 다른 하이퍼파라미터를 바꾼 후에는 학습률을 다시 튜닝해야 한다. 여전히 성능이 높지 않으면 3) 층 개수, 층에 있는 뉴런 개수, 은닉층이 사용하는 활성화 함수와 같은 모델의 하이퍼파라미터를 튜닝해볼 수 있다. 4) 배치 크기와 같은 다른 하이퍼파라미터도 튜닝해볼 수 있다(fit() 메서드를 호출 할 때 batch_size 매개변수로 지정하고, 기본값은 32이다).
모델의 검증 정확도가 만족스럽다면 모델을 상용 환경으로 배포(deploy)하기 전 테스트 세트로 모델을 평가하여 일반화 오차를 추정해야 한다.
model.evaluate(X_test, y_test)
테스트 세트에서 하이퍼파라미터를 튜닝하려는 유혹을 참아야 한다. 그렇지 않으면 일반화 오차를 매우 낙관적으로 추정하게 된다.
모델을 사용해 예측 만들기
X_new = X_test[:3]
y_proba = model.predict(X_new) # 각 샘플에 대해 0에서 9까지 클래스마다 각각의 확률을 추정
y_proba.round(2)
가장 높은 확률을 가진 클래스에만 관심이 있다면 predict_classes() 메서드를 이용한다.
# predict_classes() 메서드는 사라짐
y_pred = np.argmax(model.predict(X_new), axis=-1)
print(y_pred)
np.array(class_names)[y_pred]
10.2.3 시퀀셜 API를 사용하여 회귀용 다층 퍼셉트론 만들기
캘리포니아 주택 가격 데이터셋으로 회귀 신경망을 구성해보자.
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
housing = fetch_california_housing()
X_train_full, X_test, y_train_full, y_test = train_test_split(housing.data, housing.target)
X_train, X_valid, y_train, y_valid = train_test_split(X_train_full, y_train_full)
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_valid = scaler.transform(X_valid)
X_test = scaler.transform(X_test)model = keras.models.Sequential([
keras.layers.Dense(30, activation='relu', input_shape=X_train.shape[1:]),
keras.layers.Dense(1)
])
model.compile(loss='mean_squared_error', optimizer='sgd')
history = model.fit(X_train, y_train, epochs=20,
validation_data=(X_valid, y_valid))
mse_test = model.evaluate(X_test, y_test)
X_new = X_test[:3]
y_pred = model.predict(X_new)10.2.4 함수형 API를 사용해 복잡한 모델 만들기
순차적이지 않은 신경망의 한 예는 와이드 & 딥(Wide & Deep) 신경망이다. 이는 참고로 2016년 헝쯔 청의 논문2에서 소개되었다. 아래 그림과 같이 입력의 일부 또는 전체가 출력층에 바로 연결된다.
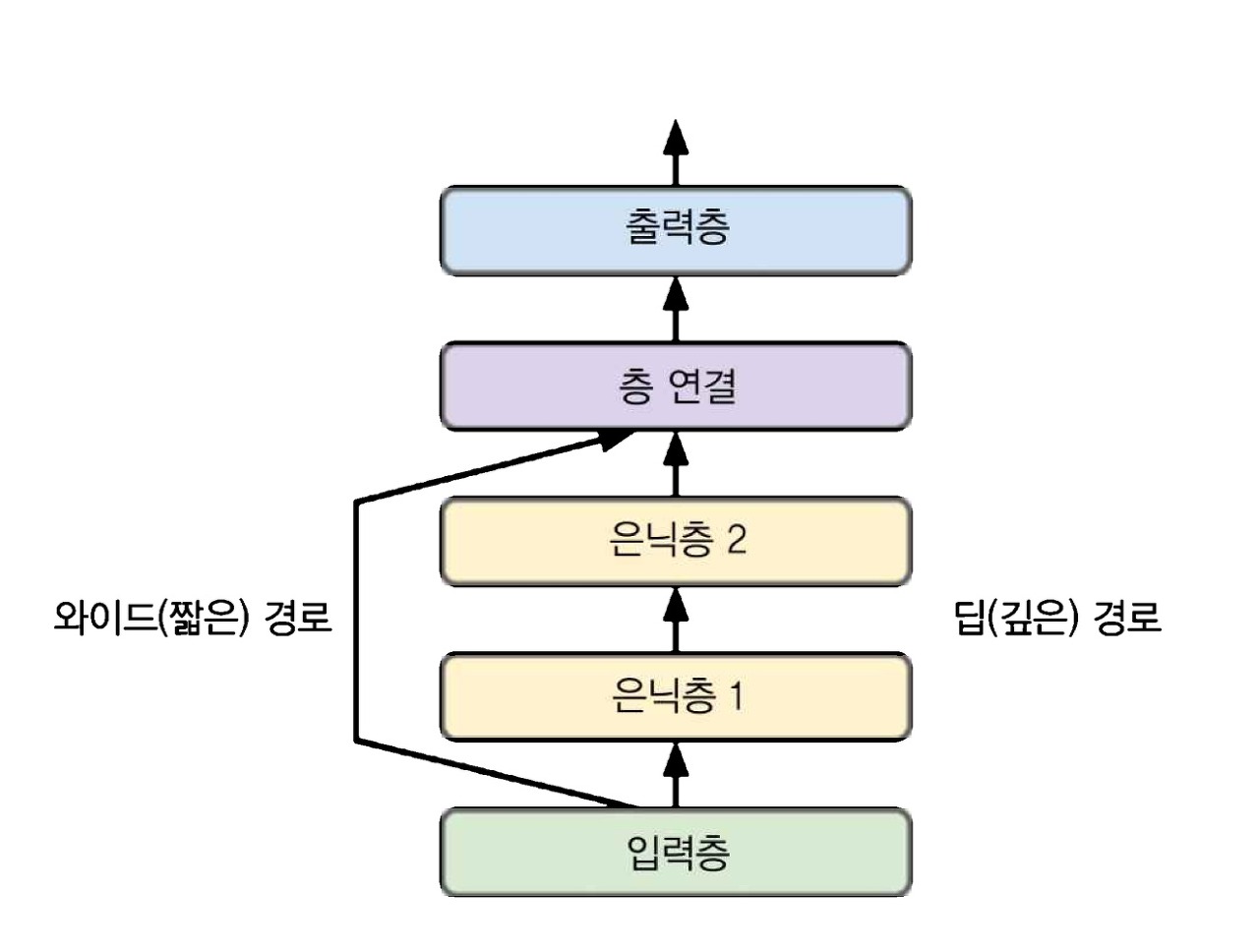
해당 구조를 사용하면 신경망이(깊게 쌓은 층을 사용한) 복잡한 패턴과 (짧은 경로를 사용한) 간단한 규칙을 모두 학습할 수 있다.
input_ = keras.layers.Input(shape=X_train.shape[1:])
hidden1 = keras.layers.Dense(30, activation='relu')(input_)
hidden2 = keras.layers.Dense(30, activation='relu')(hidden1)
concat = keras.layers.Concatenate()([input_, hidden2])
output = keras.layers.Dense(1)(concat)
model = keras.Model(inputs=[input_], outputs=[output])Input 객체: shape과 dtype을 포함하여 모델의 입력 정의
Dense 층: 이 층은 만들어지자마자 입력과 함께 함수처럼 호출되며, 이것이 함수형 API라고 부르는 이유
Concatenate 층: 함수처럼 호출하여 두 번째 은닉층의 출력과 입력을 연결
이때 일부 특성은 짧은 경로로 전달하고, 다른 특성들은(중복 가능) 깊은 경로로 전달할 수도 있다. 예를 들어 5개 특성(인덱스 0~4)을 짧은 경로로 보내고 6개 특성(인덱스 2~7)은 깊은 경로로 보낸다고 가정하자.
input_A = keras.layers.Input(shape=[5], name='wide_input')
input_B = keras.layers.Input(shape=[6], name='deep_input')
hidden1 = keras.layers.Dense(30, activation='relu')(input_B)
hidden2 = keras.layers.Dense(30, activation='relu')(hidden1)
concat = keras.layers.Concatenate([input_A, hidden2])
output = keras.layers.Dense(1, name='output')(concat)
model = keras.Model(inputs=[input_A, input_B], outputs=[output])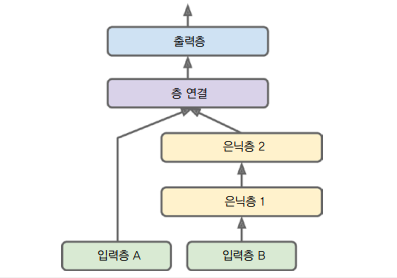
모델 컴파일은 이전과 동일하지만 fit() 메서드를 호출할 때 하나의 입력 행렬 X_train을 전달하는 것이 아니라 입력마다 하나씩 행렬의 튜플(X_train_A, X_train_B)을 전달해야 한다.
model.compile(loss='mse', optimizer=keras.optimizers.SGD(lr=1e-3))
X_train_A, X_train_B = X_train[:, :5], X_train[:, 2:]
X_valid_A, X_valid_B = X_valid[:, :5], X_valid[:, 2:]
X_test_A, X_test_B = X_test[:, :5], X_test[:, 2:]
X_new_A, X_new_B = X_test_A[:3], X_test_B[:3]
history = model.fit((X_train_A, X_train_B), y_train, epochs=20,
validation_data=((X_valid_A, X_valid_B), y_valid))
ms_test = model.evaluate((X_test_A, X_test_B), y_test)
y_pred = model.predict((X_new_A, X_new_B))
print(ms_test)
print(y_pred)
여러 개의 출력이 필요한 경우는 많다.
1. 그림에 있는 주요 물체를 분류하고 위치를 알아야 할 때(회귀 작업과 분류 작업을 함께 하는 경우)
2. 동일한 데이터에서 독립적인 여러 작업을 수행할 때(얼굴 사진을 보고 한 출력은 사람의 얼굴 표정을 분류하고, 다른 출력은 안경 착용 여부를 구별)
3. 규제 기법으로 사용할 때(신경망 구조 안에 보조 출력을 추가하여 하위 네트워크가 나머지 네트워크에 의존하지 않고 그 자체로 유용한 것을 학습하는지 확인)

output =keras.layers.Dense(1, name='main_ouput')(concat)
aux_output = keras.layers.Dense(1, name='aux_output')(hidden2)
model = keras.Model(inputs=[input_A, input_B], outputs=[output, aux_output])각 출력은 자신만의 손실 함수가 필요하다. 따라서 모델을 컴파일할 때 손실의 리스트를 전달해야 하는데, 하나의 손실을 전달하면 케라스는 모든 출력의 손실 함수가 동일하다고 가정한다.
기본적으로 케라스는 나열된 손실을 모두 합하여 최종 손실을 구해 훈련에 사용하기 때문에 보조 출력보다 주 출력에 더 관심이 많다면(보조 출력은 규제용), 주 출력의 손실에 더 많은 가중치를 부여해야 한다.
model.compile(loss=['mse', 'mse'], loss_weights=[0.9, 0.1], optimizer='sgd')모델을 훈련할 때 각 출력에 대한 레이블도 제공해야 한다. 여기서는 주 출력과 보조 출력이 같은 것을 예측해야 하므로 동일한 레이블을 사용한다. 따라서 y_train 대신 (y_train, y_train)을 전달한다.
history = model.fit([X_train_A, X_train_B], [y_train, y_train], epochs=20,
validation_data=([X_valid_A, X_valid_B], [y_valid, y_valid]))모델을 평가하면 케라스는 개별 손실과 함께 총 손실을 반환한다.
total_loss, main_loss, aux_loss = model.evaluate([X_test_A, X_test_B], [y_test, y_test])
y_pred_main, y_pred_aux = model.predict([X_new_A, X_new_B])
print(y_pred_main)
print(y_pred_aux)
10.2.5 서브클래싱 API로 동적 모델 만들기
시퀀셜 API와 함수형 API는 모두 선언적(declarative)이어서 사용할 층과 연결 방식을 먼저 정의해야 한다. 반대로 명령형(imperative) 프로그래밍 스타일이 필요하다면 서브클래싱(subclassing) API를 사용하면 된다.
class WideAndDeepModel(kears.Model):
def __init__(self, units=30, activation='relu', **kwargs):
super().__init__(**kwargs) # 표준 매개변수 처리(예: name)
self.hidden1 = keras.layers.Dense(units, activation=activation)
self.hidden2 = keras.layers.Dense(units, activation=activation)
self.main_output = keras.layers.Dense(1)
self.aux_output = keras.layers.Dense(1)
def call(self, inputs):
input_A, input_B = inputs
hidden1 = self.hidden1(input_B)
hidden2 = self.hidden2(hidden1)
concat = keras.layers.concatenate([input_A, hidden2])
main_output = self.main_output(concat)
aux_output = self.aux_output(hidden2)
return main_output, aux_output
model = WideAndDeepModel()케라스 모델에는 output이라는 속성이 있어 이를 주 출력층의 이름으로 사용할 수 없다. 따라서 main_output 이라는 이름을 사용한 것이다.
위 예제는 함수형 API와 매우 비슷하지만 Input 클래스의 객체를 만들 필요가 없다. 대신 call() 메서드의 input 매개변수를 사용한다. 생성자에 있는 층 구성과 call() 메서드에 있는 정방향 계산을 분리했다.
10.2.6 모델 저장과 복원
시퀀셜 API와 함수형 API를 사용할 경우 훈련된 모델을 저장하고 불러오는 방법은 아래와 같다.
model.save('my_keras_model.h5')
model = keras.models.load_model('my_keras_model.h5')케라스는 HDF5 포맷을 사용하여 1) 모델 구조, 2) 층의 모든 모델 파라미터, 3) 옵티마이저를 저장하게 된다. 훈련이 몇 시간 동안 지속되는 경우 훈련 도중 일정 간격으로 체크포인트(checkpoint)를 저장해야 한다. 이때 fit() 메서드의 콜백(callback)을 사용하면 된다.
추가
fit() iteraion 시 특정 이벤트가 발생할 때마다 등록된 콜백이 호출되어 수행하는 방식이다. 주로 최적의 Learning rate를 관리하는데 사용된다.
사용자는 콜백 API를 등록하는 것이고, 호출은 model.fit() 가 수행하는 것이다.
10.2.7. 콜백 사용하기
ModelCheckpoint 는 훈련하는 동안 일정한 간격으로 모델의 체크포인트를 저장한다. 기본적으로 매 에포크의 끝에서 호출된다.
checkpoint_cb = keras.callbacks.ModelCheckpoint('my_keras_model.h5')
history = model.fit(X_train, y_train, epochs=10, callbacks=[checkpoint_cb])훈련하는 동안 검증 세트를 사용하면 ModelCheckpoint 를 만들 때 save_best_only=True 로 지정할 수 있다. 이렇게 하면 최상의 검증 세트 점수에서만 모델을 저장하게 된다.
checkpoint_cb = keras.callbacks.ModelCheckpoint('my_keras_model.h5', save_best_only=True)
history = model.fit(X_train, y_train, epochs=10, validation_data=(X_valid, y_valid), callbacks=[checkpoint_cb])
model = keras.models.load_model('my_keras_model.h5') # 최상의 모델로 복원조기 종료를 구현하는 또 다른 방법은 EarlyStopping 콜백을 사용하는 것이다. 일정 에포크(patience 매개변수로 지정) 동안 검증 세트에 대한 점수가 향상되지 않으면 훈련을 멈춘다.
# EarlyStopping(monitor='val_loss', min_delta=0, patience=0, verbose=0, mode='auto', baseline=None, restore_best_weights=False)
early_stopping_cb = keras.callbacks.EarlyStopping(patience=10, restore_best_weights=True)
history = model.fit(X_train, y_train, epochs=100,
validation_data=(X_valid, y_valid),
callbacks=[checkpoint_cb, early_stopping_cb])
monitor: 모니터할 지표(loss 또는 평가 지표)
patience: Early Stopping 적용 전에 모니터할 에포크 횟수
mode: {auto, min, max} 중 하나
- 모니터 지표가 감소해야 좋을 경우 min, 증가해야 좋을 경우 max, auto는 모니터 이름에서 유추
모델이 향상되지 않으면 훈련이 자동으로 중지되므로 에포크 숫자를 크게 지정해도 된다. 또한 위의 경우 훈련이 끝난 후 최상의 가중치를 복원하기 때문에 저장된 모델을 따로 복원할 필요가 없다.
더 많은 제어가 필요하면 사용자 정의 콜백을 만들 수 있다. 예를 들어 아래의 경우 훈련하는 동안 검증 손실과 훈련 손실의 비율을 출력한다(오버피팅 감지용).
class PrintValTrainRatioCallback(keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs):
print('\nval/train: {:.2f}'.format(logs['val_loss'] / logs['loss']))콜백 메서드의 파라미터는 다양하기 때문에 상황에 맞춰 커스터마이징 할 수 있다. 훈련, 평가, 예측 등에 사용되는 함수들도 살펴보려면 공식 문서를 참고하자.
10.3 신경망 하이퍼파라미터 튜닝하기
신경망의 유연성은 단점이기도 하다. 조절할 하이퍼파라미터가 많기 때문인데 어떤 조합이 주어진 문제에서 최적인지 알 수 있을까?
한 가지 방법은 많은 하이퍼파라미터 조합을 시도해보고 어떤 것이 검증 세트에서(또는 K-폴드 교차 검증) 가장 좋은 점수를 내는지 확인하는 것이다. GridsearchCV 나 RandomizedSearchCV 를 사용해 하이퍼파라미터 공간을 탐색할 수 있다.
def build_model(n_hidden=1, n_neurons=30, learning_rate=3e-3, input_shape=[8]):
model = keras.models.Sequential()
model.add(keras.layers.InputLayer(input_shape=input_shape))
for layer in range(n_hidden):
model.add(keras.layers.Dense(n_neurons, activation='relu'))
model.add(keras.layers.Dense(1))
optimizer = keras.optimizer.SGD(lr=learning_rate)
model.compile(loss='mse', optimizer=optimizer)
return model아래처럼 KerasRegressor 객체를 만들면 일반적인 사이킷런 회귀 추정기처럼 사용할 수 있다.
keras_reg = keras.wrappers.scikit_learn.KerasRegressor(build_model) # build_model() 함수로 만들어진 케라스 모델을 감싸는 간단한 wrapperkeras_reg.fit(X_train, y_train, epochs=100,
validation_data=(X_valid, y_valid),
callbacks=[keras.callbacks.EarlyStopping(patience=10)])
mse_test = keras_reg.score(X_test, y_test)
y_pred = keras_reg.predict(X_new)모델 하나를 훈련하고 평가하려는 것이 아니라 수백 개의 모델을 훈련하고 검증 세트에서 최상의 모델을 선택해야 한다. 하이퍼파라미터가 많으므로 그리드 탐색보단 랜덤 탐색을 사용하는 것이 좋다.
from scipy.stats import reciprocal # 상호연속랜덤변수: reciprocal.pdf(x, a, b) = 1 / (x*log(b/a))
from sklearn.model_selection import RandomizedSearchCV
param_distribs = {
'n_hidden': [0, 1, 2, 3],
'n_neurons': np.arange(1, 100),
'learning_rate': reciprocal(3e-4, 3e-2)
}
rnd_search_cv = RandomizedSearchCV(keras_reg, param_distribs, n_iter=10, cv=3)
rnd_search_cv.fit(X_train, y_train, epochs=100,
validation_data=(X_valid, y_valid),
callbacks=[keras.callbacks.EarlyStopping(patience=10)])RandomizedSearchCV 는 k-겹 교차 검증을 사용하기 때문에 X_valid와 y_valid를 사용하지 않는다. 단지 조기 종료에만 사용될 뿐이다.
print(rnd_search_cv.best_params_)
print(rnd_search_cv.best_score_)
model = rnd_search_cv.best_estimator_.model하이퍼파라미터 최적화에 사용할 수 있는 파이썬 라이브러리는 아래와 같이 다양하다. 핵심 아이디어는 간단한데, 바로 탐색 지역이 좋다고 판명될 때 더 탐색을 수행하는 것이다.
1. Hyperopt
- (학습률과 같은 실수와 층의 개수 같은 이산적인 값 포함) 모든 종류의 복잡한 탐색 공간에 대해 최적화를 수행
2. Hyperas, kpot, Talos
- 케라스 모델을 위한 하이퍼파라미터 최적화 라이브러리
3. 케라스 튜너(Keras Tuner)
- 구글이 개발한 케라스 하이퍼파라미터 최적화 라이브러리
4. Scikit-Optimize(skopt)
- 범용 최적화 라이브러리로 BayesSearchCV 클래스는 GridSearchCV와 비슷한 인터페이스를 사용하여 베이즈(Bayesian) 최적화 수행
5. Spearmint
- 베이즈 최적화 라이브러리
6. Hyperband
- 리샤 리(Lisha Li) 등의 "Hyperband" 논문3을 기반으로 구축된 빠른 하이퍼파라미터 튜닝 라이브러리
7. Sklearn-Deap
- GridSearchCV와 비슷한 인터페이스를 가진 진화 알고리즘 기반의 최적화 라이브러리
10.3.1 은닉층 개수
은닉층 하나로 시작해도 많은 문제에서 납득할 만한 결과를 얻을 수 있다. 하지만 복잡한 문제에선 심층 신경망이 얕은 신경망보다 파라미터 효율성(parameter efficiency)이 훨씬 좋다. 심층 신경망은 복잡한 함수를 모델링하는 데 얕은 신경망보다 훨씬 적은 수의 뉴런을 사용하므로 동일한 양의 훈련 데이터에서 더 높은 성능을 낼 수 있다.
대규모 이미지 분류나 음성 인식같이 매우 복잡한 작업에서는 일반적으로 수십 개 층으로 이뤄진 네트워크가 필요하다. 그리고 훈련 데이터가 많이 필요한데, 이런 네트워크를 처음부터 훈련하는 경우는 드물다. 비슷한 작업에서 가장 뛰어난 성능을 낸 미리 훈련된 네트워크 일부를 재사용하는 것이 일반적이다. 이런 방법을 전이 학습(transfer learning)이라고 한다.
10.3.2 은닉층의 뉴런 개수
실전에서는 필요한 것보다 더 많은 층과 뉴런을 가진 모델을 선택하고, 그런 다음 오버피팅되지 않도록 조기 종료나 규제 기법을 사용하는 것이 간단하고 효과적이다. 구글의 과학자 빈센트 반호크(Vincent Vanhoucke)는 이를 "스트레치 팬츠(stretch pants)"라고 불렀다. 즉 나에게 맞는 사이즈의 바지를 찾느라 시간을 낭비하는 대신 그냥 큰 스트레치 팬츠를 사고 나중에 알맞게 줄이는 것이다.
10.3.3 학습률, 배치 크기 그리고 다른 하이퍼파라미터
1. 학습률
- 좋은 학습률을 찾는 한 가지 방법은 매우 낮은 학습률(예: 10−5)에서 시작해서 점진적으로 매우 큰 학습률(예: 10)까지 수백 번 반복하여 모델을 훈련하는 것이다. 이때 반복마다 일정한 값을 학습률에 곱한다.
2. 옵티마이저
- 고전적인 평범한 미니배치 경사 하강법보다 더 좋은 옵티마이저를 선택하는 것도 매우 중요하다.
3. 배치 크기
- 배치 크기는 모델 성능과 훈련 시간에 큰 영향을 미칠 수 있다. 큰 배치 크기를 사용하면 초당 더 많은 샘플을 처리할 수 있지만, 실전에선 훈련 초기에 종종 불안정하게 훈련된다. 그래서 작은 배치 크기로 훈련된 모델만큼 일반화 성능을 내지 못할 수 있다.
- 반면, 작은 학습률로 훈련을 시작해 점점 커지는 학습률 예열(warming up)을 통해 일반화 성능에 영향을 미치지 않고 훈련 시간을 단축하기도 한다. 따라서 한 가지 전략은 학습률 예열을 사용해 큰 배치 크기를 시도하고, 만약 훈련이 불안정하거나 최종 성능이 만족스럽지 못하면 작은 배치 크기를 사용하는 것이다.
- 해당 논문4에선 큰 배치 크기보단 작은 배치 크기를 적용하는 것이 성능이 더 좋다고 말한다. 구체적으로는 8보다 크고 32보다 작게 설정하는 것을 권고한다.
4. 활성화 함수
- 일반적으로 ReLU 활성화 함수가 모든 은닉층에 좋은 기본값이다.
5. 반복 횟수
- 대부분의 경우 훈련 반복 횟수는 튜닝할 필요가 없고, 대신 조기 종료를 사용한다.
'문돌이 존버 > 데이터 분석' 카테고리의 다른 글
| (Explainable AI) 변수 상호작용 개념 이해하기 (0) | 2021.08.26 |
|---|---|
| (Explainable AI) Accumulated Local Effects Plot 개념 이해하기 (5) | 2021.08.20 |
| (Explainable AI) Individual Condition Expectation 개념 이해하기 (0) | 2021.08.17 |
| 시퀀스-투-시퀀스(sequence-to-sequence) 간단히 이해하기 (0) | 2021.08.16 |
| (Explainable AI) Partial Dependence Plot 개념 이해하기 (0) | 2021.08.09 |



