어텐션 메커니즘(Attention Mechanism) 간단히 이해하기

본 글은 "딥 러닝을 이용한 자연어 처리 입문"을 학습하며 작성한 것입니다. 중간중간 제가 이해한 내용을 좀 더 풀어서 썼습니다.

어텐션 메커니즘

RNN에 기반한 언어 모델은 크게 2가지 문제가 있습니다.

1. 하나의 고정된 크기 벡터에 모든 정보를 압축하려고 하니 정보 손실이 발생
2. RNN의 고질적인 문제인 기울기 소실(Vanishing Gradient) 문제 존재

이로 인해 기계 번역 분야에서 입력 문장이 길어지면 번역 품질이 떨어지는 현상이 나타납니다. 이를 해결하기 위해 등장한 기법이 바로 어텐션(attention)입니다.

어텐션 기본 아이디어는 디코더에서 출력 단어를 예측하는 매 시점(time step)마다, 인코더에서의 전체 입력 문장을 다시 한 번 참고하는 것입니다. 다만, 모두 동일한 비율로 참고하는 것이 아니라, 해당 시점에서 예측해야 할 단어와 연관성 있는 입력 단어 부분을 좀 더 집중해서 봅니다.

<출처: 딥 러닝을 이용한 자연어 처리 입문>

위에서 소프트맥스 층을 거쳐 나온 붉은색 사각형은 단어 각각이 출력 단어를 예측할 때 얼마나 도움이 되는지의 정도를 수치화한 것입니다. 해당 수치는 하나의 정보로 담겨(위의 초록색 삼각형) 디코더로 전송됩니다. 결과적으로 디코더가 출력 단어를 더 정확하게 예측할 확률이 높아지게 됩니다.

어텐션 함수
Attention(Q, K, V) = Attention Value
Q = Query : t 시점의 디코더 셀에서의 은닉 상태
K = Keys : 모든 시점의 인코더 셀의 은닉 상태들
V = Values : 모든 시점의 인코더 셀의 은닉 상태들

1. 쿼리에 대해 모든 키와의 유사도를 구함
2. 해당 유사도를 키와 매핑되어 있는 각각의 값(value)에 반영
3. 이렇게 유사도가 반영된 값을 모두 더해 리턴(Attention Value)

1) 어텐션 스코어(Attention Score) 구하기

아래 그림을 보면 각 입력 단어의 은닉 상태와 디코더의 현재 시점 t에서의 은닉 상태 간 내적(dot product)을 수행합니다. 주황색 박스로 된 $h_i$가 인코더의 은닉 상태고, 초록색 박스로 된 $s_t$가 디코더의 은닉 상태를 가리킵니다.

<출처: 딥 러닝을 이용한 자연어 처리 입문>

기존의 디코더는 현재 시점 t에서 2개의 입력값을 필요로 했습니다. 하나는 이전 시점 t-1의 은닉 상태와 다른 하나는 이전 시점 t-1에서 나온 출력 단어입니다. 하지만 어텐션 메커니즘에선 어텐션 값(Attention Value)이라는 새로운 값을 추가로 필요로 합니다. 어텐션 값을 설명하기 이전에 어텐션 스코어를 먼저 이야기하겠습니다.

어텐션 스코어란 현재 디코더 시점 t에서 단어를 예측하기 위해, 인코더의 모든 은닉 상태 각각이 디코더의 현 시점 은닉 상태 $s_t$와 얼마나 유사한지를 판단하는 스코어값입니다. 위에서 잠깐 설명드렸듯이, 모든 단어를 동일한 비율로 참고하지 않고 연관성 있는 입력 단어 부분을 집중(attention!)해서 본다고 했었죠.

어텐션 스코어에는 대표적으로 닷-프로덕트(dot-product) 어텐션과 바다나우 어텐션(Bahdanau Attention)이 있는데요. 본 글에선 닷-프로덕트 어텐션을 살펴보도록 하겠습니다.

닷-프로덕트 어텐션

디코더 은닉 상태인 $s_t$를 전치(transpose)하고 각 은닉 상태와 내적(dot-product)을 수행합니다. 예를 들어, $s_t$와 인코더의 i번째 은닉 상태의 어텐션 스코어 계산 모습은 아래와 같습니다.

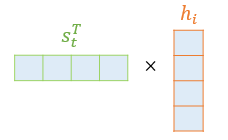
어텐션 스코어 함수 식은 아래와 같습니다.

$score(s_t, h_i) = s_t^T h_N$

$s_t$와 인코더의 모든 은닉 상태의 어텐션 스코어 모음값을 $e^t$라고 정의하면 $e^t$ 수식은 다음과 같습니다.

$e^t = [s_t^T h_1, ..., s_t^T h_N]$
여기서 N은 입력 단어 갯수, 위에선 "I am a student"로 총 4개

2) 어텐션 분포(Attention Distribution) 구하기

<출처: 딥 러닝을 이용한 자연어 처리 입문>

위에서 구한 $e^t$에 소프트맥스 함수를 적용하면 모든 값을 합했을 때 1이 되는 확률 분포를 얻게 됩니다. 이를 어텐션 분포라 하며, 각각의 값은 어텐션 가중치(Attention Weight)라고 합니다. 위 그림에서 붉은색 사각형의 크기가 가중치 크기를 나타내고 있습니다. 크기로 보면 "am", "student"가 동일한 가중치를 가지고 있음을 알 수 있죠.

디코더 시점 t에서의 어텐션 가중치 모음값인 어텐션 분포를 $\alpha_t$라고 할 때, 아래와 같이 표현할 수 있습니다.

$\alpha_t = softmax(e^t)$

 

3) 어텐션 값(Attention Value) 구하기

<출처: 딥 러닝을 이용한 자연어 처리 입문>

이제 어텐션의 최종 결과값을 얻기 위해 각 인코더의 은닉 상태와 어텐션 가중치값들을 곱하고 모두 더합니다. 이때 나오는 값이 어텐션 값이 되며 이를 $a_t$라고 하겠습니다.

$a_t = \sum_{i=1}^N \alpha_i^t h_i$

어텐션 값은 인코더의 문맥을 담고 있다고 해서 컨텍스트 벡터(context vector)라고도 불립니다.

4) 어텐션 값과 디코더 t 시점의 은닉 상태 연결(Concatenate)

<출처: 딥 러닝을 이용한 자연어 처리 입문>

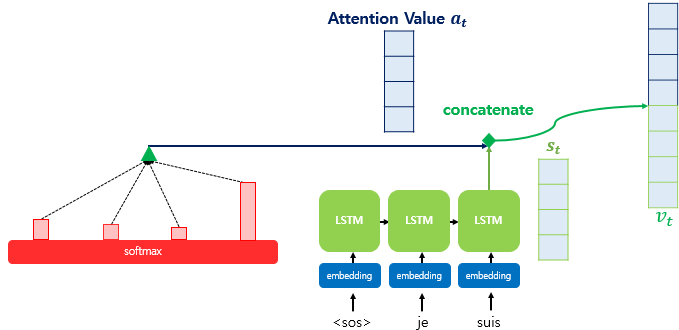
어텐션 값이 구해지면 $a_t$를 $s_t$와 결합(concatenate)하여 하나의 벡터로 만드는 작업을 수행하며, 이를 $v_t$로 정의합니다. $v_t$는 $\hat{y}$ 예측 연산의 입력으로 사용하여 인코더로부터 얻은 정보를 활용해 $\hat{y}$를 좀 더 잘 예측할 수 있게 합니다(여기서 끝이 아닙니다!!).

5) 출력층 연산의 입력인 $\tilde{s_t}$

어텐션 매커니즘에선 위에서 구한 $v_t$를 바로 출력층으로 보내지 않고 그 전에 신경망 연산을 추가합니다. 가중치 행렬과 곱한 후 하이퍼볼릭탄젠트 함수를 지나도록 하여 출력층 연산을 위한 새로운 벡터인 $\tilde{s_t}$를 얻습니다.

<출처: 딥 러닝을 이용한 자연어 처리 입문>

식으로 표현하자면 아래와 같습니다.

$\tilde{s_t} = tanh(W_c[a_t;s_t] + b_c)$
$W_c$는 학습 가능한 가중치 행렬, $b_c$는 편향
$[a_t;s_t]$는 위에서 결합한 벡터 $v_t$를 가리킴

이때 가중치 행렬 $W_c$의 크기는 (4, 8), 즉 위에서 설정한 (은닉 상태 크기, 은닉 상태 크기 x 2)입니다. $v_t$의 크기가 연결을 통해 (은닉 상태 크기 x 2, 1)이 되었기 때문입니다. 어텐션을 소개한 논문^[각주:1]에서는 위의 과정이 아래와 같은 수식으로 표현되었습니다.

$s_i = f(s_{i-1}, y_{i-1}, c_i)$

$s_i$: i번째 시점의 은닉 상태
$y_{i-1}$: i-1번째 타겟 단어(or 예측 단어)
$c_i$: i번째 시점의 컨텍스트 벡터

마지막으로 $\tilde{s_t}$를 출력층의 입력으로 사용하여 예측 벡터를 계산한 후 소프트맥스를 적용하면 다음 예측 단어를 추론할 수 있습니다.

$\hat{y_t} = Softmax(W_y\tilde{s_t} + b_y)$

위의 과정을 한눈에 이해할 수 없을까 구글링을 하다가 (B급 개발님이 수고해주신) 어텐션 메커니즘을 정말 잘 그린 도식을 찾았습니다.

출처: [Pytorch] 차근차근 구현하는 seq2seq + attention mechanism (tistory.com)

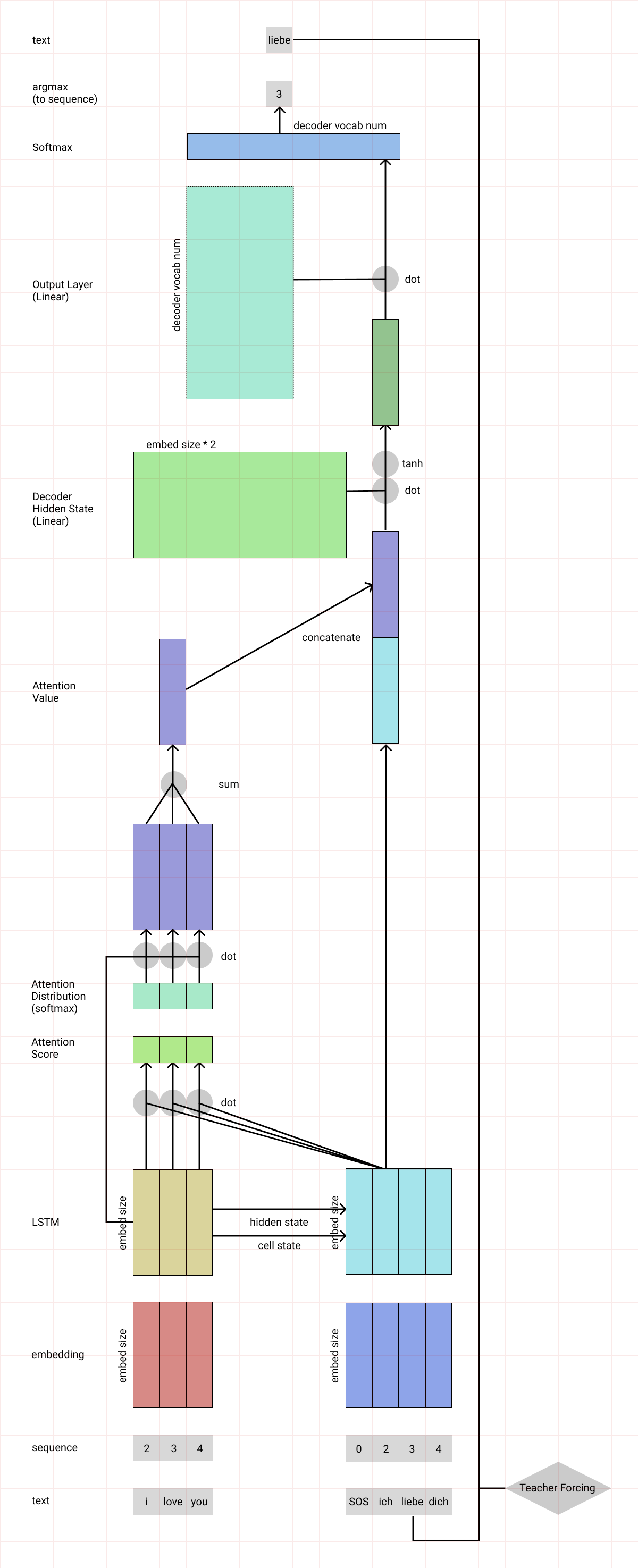
참고로 어텐션의 종류는 다양하다고 합니다. 어텐션 차이는 중간 수식인 어텐션 스코어 함수 차이를 말하는데, 저희가 위에서 살펴본 것은 내적을 사용한 닷-프로덕트 어텐션이었습니다. 어텐션 스코어를 구하는 방법은 여러가지가 제시되었으며 자세한 것은 아래를 참고해주시면 되겠습니다.

<출처: 딥 러닝을 이용한 자연어 처리 입문>

다음은 바다나우 어텐션(Bahdanau attention)을 소개하도록 하겠습니다.

참조
딥 러닝을 이용한 자연어 처리 입문(https://wikidocs.net/22893)

1. NEURAL MACHINE TRANSLATION BY JOINTLY LEARNING TO ALIGN AND TRANSLATE [본문으로]