비지도 학습
8장에서 가장 널리 사용되는 비지도 학습 방법인 차원 축소를 살펴보았다. 9장에서는 크게 아래의 비지도 학습 알고리즘을 배울 예정이다.
1. 군집(clustering)
비슷한 샘플을 클러스터로 모은다. 군집은 데이터 분석, 고객 분류, 추천 시스템, 검색 엔진, 이미지 분할, 준지도 학습, 차원 축소 등에 사용할 수 있다.
2. 이상치 탐지(outlier detection)
'정상' 데이터가 어떻게 보이는지 학습한다. 그 다음 비정상 샘플을 감지하는 데 사용한다. 예를 들어, 제조 라인에서 결함 제품을 감지하거나 시계열 데이터에서 새로운 트랜드를 찾는다.
3. 밀도 추정(density estimation)
데이터셋 생성 확률 과정(random process)의 확률 밀도 함수(probabilty density function)를 추정한다. 밀도 추정은 이상치 탐지에 널리 사용된다. 밀도가 매우 낮은 영역에 놓인 샘플이 이상치일 가능성이 높다. 데이터 분석과 시각화에도 유용하다.
9.1 군집
비지도 학습은 기본적으로 데이터에 라벨링이 되어 있지 않다. 붓꽃 데이터를 예로 들면, 특정 샘플이 Iris setosa 인지, Iris versicolor 인지 모르는 상황이다. 먼저, 군집에 대해 알아보자.
군집은 아래와 같은 다양한 애플리케이션에 사용된다.
1. 고객 분류
고객을 구매 이력이나 웹사이트 내 행동 등을 기반으로 클러스터로 모을 수 있다. 이는 고객이 누구인지, 고객이 무엇을 원하는지 이해하는 데 도움이 된다. 고객 그룹마다 제품 추천이나 마케팅 전략을 다르게 적용할 수 있다. 예를 들어, 동일한 클러스터 내 사용자가 좋아하는 컨텐츠를 추천하는 추천 시스템(recommender system)을 만들 수 있다.
2. 데이터 분석
새로운 데이터셋을 분석할 때 군집 알고리즘을 실행하고 각 클러스터를 따로 분석하면 도움이 된다.
3. 차원 축소 기법
한 데이터셋에 군집 알고리즘을 적용하면 각 클러스터에 대한 샘플의 친화성(affinity)을 측정할 수 있다(친화성은 샘플이 클러스터에 얼마나 잘 맞는지 측정). 각 샘플의 특성 벡터 x는 클러스터 친화성의 벡터로 바꿀 수 있다. k개의 클러스터가 있다면 이 벡터는 k차원이 된다. 이 벡터는 일반적으로 원본 특성 벡터보다 훨씬 저차원이지만, 분석을 위한 충분한 정보를 가질 수 있다.
4. 이상치 탐지
모든 클러스터에 친화성이 낮은 샘플은 이상치일 가능성이 높다. 웹사이트 내 행동을 기반으로 사용자의 클러스터를 만들었다면 초당 웹서버 요청을 비정상적으로 많이 하는 사용자를 감지할 수 있다. 이상치 탐지는 특히 제조 분야에서 결함을 감지할 때 혹은 부정 거래 감지(fraud detector)에 활용된다.
5. 준지도 학습
라벨링된 샘플이 적다면 군집을 수행하고 동일한 클러스터에 있는 모든 샘플에 라벨을 전파할 수 있다.
6. 검색 엔진
일부 검색 엔진은 제시된 이미지와 비슷한 이미지를 찾아준다. 이런 시스템을 구축하려면 먼저 데이터베이스에 있는 모든 이미지에 군집 알고리즘을 적용해야 한다. 비슷한 이미지는 동일한 클러스터에 속한다. 사용자가 찾으려는 이미지를 제공하면 훈련된 군집 모델을 사용해 이미지의 클러스터를 찾는다. 그다음 해당 클러스터의 모든 이미지를 반환한다.
7. 이미지 분할
색을 기반으로 픽셀을 클러스터로 모은다. 그다음 각 픽셀의 색을 해당 클러스터의 평균 색으로 바꿔준다. 이는 이미지에 있는 색상의 종류를 크게 줄이고, 이로써 하면 물체의 윤곽을 감지하기 쉬워져 물체 탐지 및 추적 시스템에서 이미지 분할을 많이 활용한다.
9.1.1 K-평균
K-평균은 각 클러스터의 중심, 즉 센트로이드(centroid)를 찾고 가장 가까운 클러스터에 샘플을 할당한다.
from sklearn.cluster import KMeans
k = 5
kmeans = KMeans(n_clusters=k)
y_pred = kmenas.fit_predict(X)알고리즘이 찾을 클러스터 개수 k를 지정해야 하지만 일반적으로 적절한 개수를 찾는 것이 쉬운 일은 아니다. 이와 관련해선 뒤에서 다시 설명하도록 한다.
y_pred
# array([4, 0, 1, ...., 2, 1, 0], dtype=int32)
y_pred is kmeans.labels_
# True
kmeans.cluster_centers_
# array([[-2.80389616, 1.80117999],
# [ 0.20876306, 2.25551336],
# [-2.79290307, 2.79641063],
# [-1.46679593, 2.28585348],
# [-2.80037642, 1.30082566]])KMeans 클래스의 인스턴스는 labels_ 인스턴스 변수에 훈련된 샘플의 라벨을 가지고 있다.
실제 K-평균 알고리즘은 클러스터 크기가 많이 다르면 잘 작동하지 않는다. 샘플을 클러스터에 할당할 때 센트로이드까지 거리를 고려하는 것이 전부기 때문이다.
하드 군집(hard clustering)이라는 샘플을 하나의 클러스터에 할당하는 것보다 클러스터마다 샘플에 점수를 부여하는 것이 유용할 수 있다. 이를 소프트 군집(soft clustering)이라고 하며, 이 점수는 샘플과 센트로이드 사이의 거리가 될 수 있다. KMeans 클래스의 transform() 메서드는 샘플과 각 센트로리드 사이의 거리를 반환한다.
kmeans.transform(X_new)
K-평균 알고리즘
처음에는 센트로이드를 랜덤하게 선정한다(예를 들어, 무작위로 k개의 샘플을 뽑아 그 위치를 센트로이드로 정함). 그다음 샘플에 라벨을 할당하고 센트로이드를 업데이트하고, 샘플에 라벨을 할당하고 센트로이드를 업데이트하는 식으로 센트로이드에 변화가 없을 때까지 계속한다.
이는 무한 반복될 것으로 보이지만 사실 제한된 횟수 안에 수렴하는 것을 보장한다. 물론, 이것이 지역 최적점(local minimum)으로 수렴할 수 있기 때문에 최적의(best) 솔루션이라고는 보장하지 못한다. 최적의 솔루션은 사실 센트로이드를 초기에 어느 곳에 위치하느냐에 달려 있다.
센트로이드 초기화 방법
센트로이드 위치를 근사하게 알 수 있다면(예를 들어, 또 다른 군집 알고리즘 우선 실행) init 매개변수에 센트로이드 리스트를 담은 넘파이 배열을 지정하고 n_init을 1로 설정할 수 있다.
good_init = np.array([[-3, 3], [-3, 2], [-3, 1], [-1, 2], [0, 2]])
kmeans = KMeans(n_clusters=5, init=good_init, n_init=1)또 다른 방법은 랜덤 초기화를 다르게 하여 여러 번 알고리즘을 실행하고 가장 좋은 솔루션을 선택하는 것이다. 랜덤 초기화는 n_init 매개변수로 조절하며 디폴트값은 10이다. 알고리즘이 10번 실행되면 사이킷런은 이 중에 최선의 솔루션을 반환한다. 이때 사용하는 성능 지표가 있는데, 이 값은 각 샘플과 가장 가까운 센트로이드 사이의 평균 제곱 거리이며 모델의 이너셔(inertia)라고 부른다.
kmeans.inertia_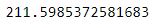
score() 메서드는 이너셔의 음숫값을 반환한다. 예측기의 score() 메서드는 사이킷런의 '큰 값이 좋은 것이다'라는 규칙을 따르는데, 따라서 한 예측기가 다른 것보다 좋다면 score() 메서드가 더 높은 값을 반환해야 한다.
kmeans.score(X)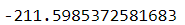
데이비드 아서(David Arthur)와 세르게이 바실비츠키(Sergei Vassilvitskii)가 2006년 논문에서 K-평균++ 알고리즘을 제안했다. 다른 센트로이드와 거리가 먼 센트로이드를 선택하는 똑똑한 초기화 단계를 소개했고, 이는 K-평균 알고리즘이 최적이 아닌 솔루션으로 수렴할 가능성을 크게 낮춘다.
1. 데이터셋에서 무작위로 균등하게 하나의 센트로이드 c(1)을 선택한다.
2. D(x(i))2/∑mj=D(x(j))2의 확률로 샘플 x(i)를 새로운 센트로이드 e(i)로 선택한다. 여기에서 D(x(i))는 샘플 x(i)와 이미 선택된 가장 가까운 센트로이드까지 거리이다. 이 확률 분포는 이미 선택한 센트로이드에서 멀리 떨어진 샘플을 다음 센트로이드로 선택할 가능성을 높인다.
3. k개의 센트로이드가 선택될 때까지 이전 단계를 반복한다.
KMeans 클래스는 기본적으로 위의 초기화 방법을 사용한다. 원래 방식으로 사용하고 싶다면 init 매개변수를 "random"으로 지정하면 되지만 굳이 이렇게 할 필요는 없다.
K-평균 속도 개선과 미니배치 K-평균
2013년 찰스 엘칸(Charles Elkan)의 논문에서 제안한 개선 방법으로 불필요한 거리 계산을 많이 피하여 알고리즘 속도를 상당히 높였다. 삼각 부등식(triangle inequality)1를 사용하였고, 이는 두 점 사이의 직선은 항상 가장 짧은 거리가 된다는 것이다. 그리고 샘플과 센트로이드 사이의 거리를 위한 하한선과 상한선을 유지한다. 해당 알고리즘은 KMeans 클래스에서 디폴트로 사용된다.
2010년 데이비드 스컬리(David Sculley)의 논문에서 또 다른 변종이 제시되었다. 전체 데이터셋을 사용해 반복하지 않고 각 반복마다 미니배치를 사용해 센트로이드를 조금씩 이동한다. 일반적으로 알고리즘 속도를 3~4배 정도 높이는 것으로 알려져 있으며, 대량의 데이터셋에 적용하기 적합하다.
사이킷런의 MiniBatchKMeans 클래스에 해당 알고리즘을 구현했다.
from sklearn.cluster import MiniBatchKMeans
minibatch_kmeans = MiniBatchKMeans(n_clusters=5)
minibatch_kmeans.fit(X)직관적으로 알 수 있듯, 미니배치 K-평균 알고리즘은 일반 K-평균 알고리즘보다 빠르지만 이너셔는 조금 더 나쁘다. 특히 클러스터 개수가 증가할 때 그렇다.
최적의 클러스터 개수 찾기
일반적으로 최적의 클러스터 개수 k를 찾는 것은 쉽지 않다. 보통 엘보(elbow) 기법이라고 해서 클러스터 개수에 따른 이너셔를 그리는 그래프가 있지만, 너무 엉성한 방법이다. 더 정확하고 동시에 계산 비용이 많이 드는 방법은 실루엣 점수(silhouette score)다. 이 값은 모든 샘플에 대한 실루엣 계수(silhouette coefficient)의 평균이다.
샘플의 실루엣 계수는 (b−a)/max(a,b)로 계산하며 범위는 -1에서 1까지다.
a: 동일한 클러스터에 있는 다른 샘플까지 평균 거리
b: 가장 가까운 클러스터까지 평균 거리
실루엣 계수가 1에 가까우면 자신의 클러스터 안에 잘 속해 있고 다른 클러스터와는 멀리 떨어져 있다는 뜻이다. 반대로 실루엣 계수가 0에 가까우면 클러스터 경계에 위치한다는 의미고, -1에 가까우면 해당 샘플이 잘못된 클러스터에 할당되었다는 의미다.
사이킷런의 silhouette_score() 함수를 사용하면 구현할 수 있다.
from sklearn.metrics import silhouette_score
silhouette_score(X, kmeans.labels_)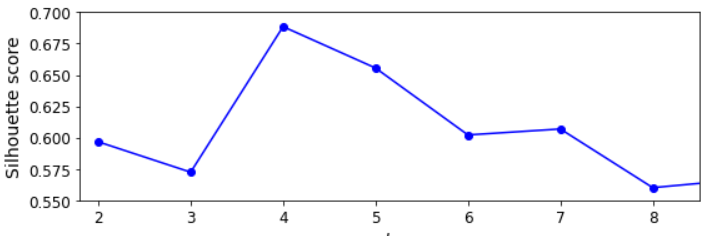
단순히 클러스터 개수에 따른 이너셔를 그린 그래프(엘보) 보다 훨씬 많은 정보를 보여준다. k=4가 좋은 선택이지만 k=6이나 7과 비교했을 때 k=5 역시 좋은 성능을 보여준다.
모든 샘플의 실루엣 계수를 할당된 클러스터와 계숫값으로 정렬하여 보여주는 실루엣 다이어그램이 있다.
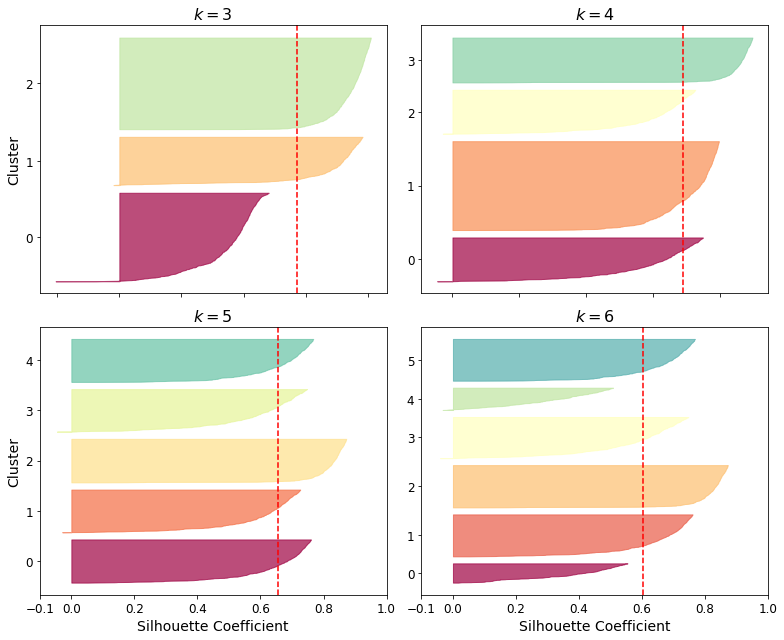
그래프의 높이는 클러스터가 포함하고 있는 샘플의 개수를 의미하고, 너비는 이 클러스터에 포함된 샘플의 정렬된 실루엣 계수를 나타낸다(넓을수록 좋다). 수직 파선은 평균 실루엣 점수를 나타낸다. 한 클러스터의 샘플 대부분이 이 점수보다 낮은 계수를 가지면 클러스터 샘플이 다른 클러스터랑 너무 가깝다는 것을 의미한다.
다이어그램을 보면 k=5일 때 모두 수직파선을 넘겼고, 클러스터 간 실루엣 계수 차이가 적기 때문에 k=4보다 k=5를 선택하는 것이 좋다.
9.1.2 K-평균의 한계
K-평균은 최적이 아닌 솔루션을 피하려면 알고리즘을 여러 번 실행해야 하고, 클러스터 개수도 지정해야 한다. 또 클러스터 크기나 밀집도가 서로 다르거나 원형이 아닐 경우 잘 작동하지 않는다.
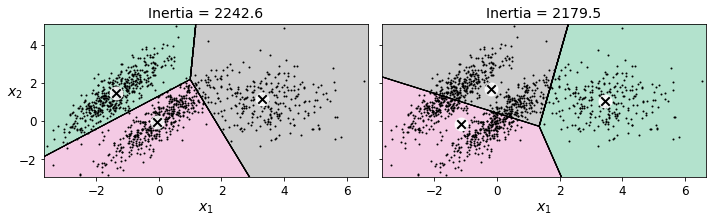
위 그래프와 같이 타원형 클러스터를 가진 데이터셋을 K-평균으로 군집하면 결과가 좋지 않다. 이때는 보통 가우시안 혼합 모델이 잘 작동한다.
K-평균을 실행하기 전 입력 특성의 스케일을 맞추는 것이 중요
9.1.3 군집을 사용한 이미지 분할
이미지 분할(image segmentation)은 이미지를 세그멘트 여러 개로 분할하는 작업이다. 시맨틱 분할(semantic segmentation)에서는 동일한 종류의 물체에 속한 모든 픽셀은 같은 세그먼트에 할당된다. 예를 들어, 자율 주행 시스템에서 보행자 이미지를 구성하는 모든 픽셀은 '보행자' 세그먼트에 할당될 것이다.
지금 살펴볼 색상 분할(color segmentation)은 동일한 색상을 가진 픽셀을 같은 세그먼트에 할당한다.
from matplotlib.image import imread # 아니면 from imageio import imread
image = imread(os.path.join("images", "unsupervised_learning", "ladybug.png"))
image.shape # (533, 800, 3)위의 이미지는 3D 배열로 표현되며, (높이, 너비, 컬러 채널 개수)를 의미한다. 컬러 채널에는 보통 RGB(빨강, 초록, 파랑) 채널이 있고, 이는 다시 말하면 각 픽셀에 대해 빨강, 초록, 파랑의 강도를 담은 3D 벡터가 있다는 것이다. 이 값은 0.0과 1.0 사이지만, imageio.imread() 를 사용한다면 0과 255 사이다.
이제 이미지 배열을 RGB 색상의 긴 리스트로 변환한 후 K-평균을 통해 색상을 클러스터로 모은다.
X = image.reshape(-1, 3)
kmeans = KMeans(n_clusters=8).fit(X)
segmented_img = kmeans.cluster_centers_[kmeans.labels_]
segmented_img = segmented_img.reshape(image.shape)
8개보다 클러스터 개수를 작게 하면 무당벌레의 빨간색이 독자적인 클러스터를 만들지 못하고 주위에 합쳐진다. 이는 K-평균이 비슷한 크기의 클러스터를 만드는 경향이 있기 때문이다.
9.1.4 군집을 사용한 전처리
군집은 차원 축소에 효과적인 방법으로, 지도 학습 알고리즘을 적용하기 전에 전처리 단계로 사용할 수 있다.
# MNIST 셋 불러오기
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
X_digits, y_digits = load_digits(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X_digits, y_digits)from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)log_reg.score(X_test, y_test)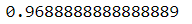
이제 K-평균을 전처리 단계로 사용하여 성능이 더 좋아는지 확인해본다.
from sklearn.pipeline import Pipeline
pipeline = Pipeline([
("kmeans", KMeans(n_clusters=50)),
("log_reg", LogisticRegression()),
])
pipeline.fit(X_train, y_train)pipeline.score(X_test, y_test)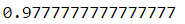
여기에 최선의 클러스터 개수 k를 찾는 일을 추가하면 되는데, 사실 K-평균을 전처리 단계로 사용하고 있기 때문에 실루엣 분석이나 엘보 기법을 사용할 필요는 없다. 교차 검증에서 가장 좋은 분류 성능을 내는 값이 가장 좋은 k 값이다.
from sklearn.model_selection imoprt GridSearchCV
param_grid = dict(kmeans_n_clusters=range(2, 100))
grid_clf = GridSearchCV(pipeline, param_grid, cv=3, verbose=2)
grid_clf.fit(X_train, y_train)
print(grid_clf.best_params_)
print(grid_clf.score(X_test, y_test))
핸즈온 머신러닝 2 깃허브에 오류가 있는 것으로 보인다. 위의 결과 성능이 향상되어야 하는데, 클러스터 개수가 50개일 때와 동일한 성능을 보여준다.
9.1.5 군집을 사용한 준지도 학습
군집은 레이블이 없는 데이터가 많고 레이블이 있는 데이터는 적을 때(준지도 학습) 역시 사용할 수 있다. 일단, 숫자 데이터셋에서 라벨링이 있는 50개 샘플에 로지스틱 회귀 모델을 훈련해본다.
n_labeled = 50
log_reg = LogistRegression()
log_reg.fit(X_train[:n_labeled], y_train[:n_labeled])
log_reg.score(X_test, y_test)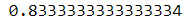
정확도를 개선하기 위해 훈련 세트를 50개의 클러스터로 모은다. 이후 각 클러스터에서 센트로이드에 가장 가까운 이미지를 찾고, 이를 대표 이미지(representative image)라고 부른다.
k = 50
kmeans = KMeans(n_clusters=k)
X_digits_dist = kmeans.fit_transform(X_train)
representative_digit_idx = np.argmin(X_digits_dist, axis=0)
X_representative_digits = X_train[representative_digit_idx]
위의 대표 이미지 50개를 보고 수동으로 라벨링을 한다. 그리고 테스트 차원에서 이를 가지고 로지스틱 회귀 모형을 돌려본다.
y_representative_digits = np.array([
0, 1, 3, 2, 7, 6, 4, 6, 9, 5,
1, 2, 9, 5, 2, 7, 8, 1, 8, 6,
3, 1, 5, 4, 5, 4, 0, 3, 2, 6,
1, 7, 7, 9, 1, 8, 6, 5, 4, 8,
5, 3, 3, 6, 7, 9, 7, 8, 4, 9])log_reg = LogisticRegression()
log_reg.fit(X_representative_digits, y_representative_digits)
log_reg.score(X_test, y_test) # 0.922222...
샘플에 라벨링하는 작업은 비용이 많이 들고 어렵기 때문에 무작위 샘플 대신 대표 샘플에 라벨링하는 것이 좋은 방법이다.
여기서 한 단계 나아가면 라벨링을 동일한 클러스터에 있는 모든 샘플로 전파하는 라벨 전파(label propogation) 방법이 있다.
y_train_propogated = np.empty(len(X_train), dtype=np.int32)
for i in range(k):
y_train_propogated[kmeans.labels_==i] = y_representative_digits[i]
log_reg = LogisticRegression()
log_reg.fit(X_train, y_train_propogated)
log_reg.score(X_test, y_test) # 0.933333...그렇게 놀라운 성능 향상은 이루어지지 않았는데, 그 이유는 클러스터 경계에 가깝게 위치한 샘플이 포함되어 있고, 아마 잘못 라벨링이 되었기 때문이다. 센트로이드와 가까운 샘플의 20%에만 라벨을 전파해보고 어떻게 되는지 확인해보자.
percentile_closest = 20
X_cluster_dist = X_digits_dist[np.arange(len(X_train)), kmeans.labels_]
for i in range(k):
in_cluster = (kmeans.labels_ == i)
cluster_dist = X_cluster_dist[in_cluster]
cutoff_distance = np.percentile(cluster_dist, percentile_closest)
above_cutoff = (X_cluster_dist > cutoff_distance)
X_cluster_dist[in_cluster & above_cutoff] = -1 # 20% 밖 샘플은 -1로 표시
partially_propagated = (X_cluster_dist != -1) # 20% 내 샘플들
X_train_partially_propagated = X_train[partially_propagated]
y_train_partially_propagated = y_train_propagated[partially_propagated]이제 부분적으로 전파한 이 데이터셋에 모델을 다시 훈련한다.
log_reg = LogisticRegression()
log_reg.fit(X_train_partially_propagated, y_train_partially_propagated)
log_reg.score(X_test, y_test) # 0.94
# 실제 데이터와 유사도 비교
np.mean(y_train_partially_propagated == y_train[partially_propagated]) # 0.98690...9.1.6 DBSCAN
이 알고리즘은 밀집된 연속적 지역을 클러스터로 정의하며, 작동 방식은 아래와 같다.
1. 알고리즘이 각 샘플에서 작은 거리인 ε(입실론) 내에 샘플이 몇 개 놓여 있는지 카운트한다. 이 지역을 샘플의 ε-이웃(neighborhoold)이라고 부른다.
2. (자기 자신 포함) ε-이웃 내에 적어도 min_samples개 샘플이 있다면 이를 핵심 샘플(core instance)로 간주한다. 즉 핵심 샘플은 밀집된 지역에 있는 샘플이다.
3. 핵심 샘플의 이웃에 있는 모든 샘플은 동일한 클러스터에 속한다. 이웃에는 다른 핵심 샘플이 포함될 수 있으며, 따라서 핵심 샘플의 이웃의 이웃은 계속해서 하나의 클러스터를 형성한다.
4. 핵심 샘플이 아니고 이웃도 아닌 샘플은 이상치로 판단한다.
DBSCAN은 모든 클러스터가 충분히 밀집되더 있고 밀집되지 않은 지역과 잘 구분될 때 좋은 성능을 낸다.
from sklearn.cluster import DBSCAN
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=1000, noise=0.05)
dbscan = DBSCAN(eps=0.05, min_samples=5)
dbscan.fit()모든 샘플의 라벨은 인스턴스 변수 labels_ 에 저장되어 있다.
dbscan.labels_일부 샘플의 클러스터 인덱스는 -1인데, 이는 알고리즘이 해당 샘플을 이상치로 판단했다는 의미다. 핵심 샘플의 인덱스는 인스턴스 변수 core_sample_indices_ 에서, 핵심 샘플 자체는 components_ 에 저장되어 있다.
len(dbscan.core.sample_indices_) # 808
dbscan.core_sample_indices_ # array([0, 4, 5, 6, ...])
dbscan.components_ # array([[-0.02136124, 0.40618608],
# [-0.84192557, 0.53058695],
# ...
# [ 0.79419406, 0.60777171]])
DBSCAN 클래스는 predict() 메서드를 제공하지 않고 fit_predict() 메서드를 제공한다. 새로운 샘플에 대해 클러스터를 예측할 수 없다. 이는 곧 사용자가 필요한 예측기를 선택해야 하는데 아래와 같이 간단하게 할 수 있다.
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=50)
knn.fit(dbscan.components, dbscan.labels_[dbscan.core_sample_indices_])X_new = np.array([[-0.5, 0], [0, 0.5], [1, -0.1], [2, 1]])
knn.predict(X_new) # array([1, 0, 1, 0])
knn.predict_proba(X_new) # array([[0.18, 0.82],
# [1. , 0. ],
# ...
# [1. , 0. ]])이 분류기를 핵심 샘플에서만 훈련했지만 최종 작업의 성능에 따라 모든 샘플에서 훈련할 수도 있고, 이상치를 제외할 수도 있다. 아래 그림은 결정 경계이고, 덧셈 기호는 X_new에 있는 샘플 4개를 나타낸다.
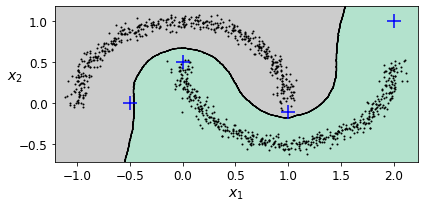
훈련 세트에 이상치가 없기 때문에 클러스터가 멀리 떨어져 있어도 분류기는 항상 클러스터 1개를 선택한다. 이때 최대 거리를 사용하면 두 클러스터에서 멀리 떨어진 샘플을 이상치로 간단히 분류할 수 있다. KNeighborsClassifier의 kneighbors() 메서드를 이용하면 된다. 이 메서드에 샘플을 전달하면 훈련 세트에서 가장 가까운 k개 이웃의 거리와 인덱스를 리턴한다.
y_dist, y_pred_idx = knn.kneighbors(X_new, n_neighbors=1)
y_pred = dbscan.labels_[dbscan.core_sample_indices_][y_pred_idx]
y_pred[y_dist > 0.2] = -1
y_pred.ravel() # array([-1, 0, 1, -1])참고로 ravel() 메서드는 다차원을 1차원으로 푸는 역할을 한다.
a1 = np.array([[1,2],
[3,4]])
a1.ravel() # array([1, 2, 3, 4])DBSCAN은 매우 간단하지만 강력한 알고리즘이다. 클러스터의 모양과 개수에 상관없이 감지할 수 있는 능력이 있고, 이상치에 안정적이며 하이퍼파라미터가 2개뿐이다(eps와 min_samples).
물론, 클러스터 간 밀집도가 크게 다르면 모든 클러스터를 올바르게 잡아내는 것이 불가능하다. 계산 복잡도는 약 O(mlogm)이고, 샘플 개수에 대해 거의 선형적으로 증가하지만 사이킷런의 구현은 eps가 커지면 O(m2)만큼 메모리가 필요하다.
9.2 가우시안 혼합
가우시안 혼합 모델(Gaussian mixture model, 이하 GMM)은 샘플이 파라미터가 알려지지 않은 여러 개의 혼합된 가우시안 분포에서 생성되었다고 가정하는 확률 모델이다. 하나의 가우시안 분포에서 생성된 모든 샘플은 하나의 클러스터를 형성하며, 일반적으로 이 클러스터는 타원형이다.
여러 GMM 변종이 있지만, 가장 간단한 버전은 GaussianMixture 클래스에 구현되어 있다. 사전에 가우시안 분포의 개수 k를 알아야 한다. 데이터셋 X가 다음 확률 과정을 통해 생성되었다고 가정한다.
1. 샘플마다 k개의 클러스터에서 랜덤하게 한 클러스터가 선택된다. j번째 클러스터를 선택할 확률은 클러스터의 가중치 ϕ(j)로 정의된다. i번째 샘플을 위해 선택한 클러스터 인덱스는 z(i)로 표시한다.
2. z(i)=j이면, 즉 i번째 샘플이 j번째 클러스터에 할당되었다면 이 샘플의 위치 x(i)는 평균이 μ(j)이고 공분산 행렬이 ∑(j)인 가우시안 분포에서 랜덤하게 샘플링된다. 이를 x(i)∼N(μ(j),∑(j))와 같이 쓴다.
위의 생성 과정은 그래프 모형으로 나타낼 수 있다. 확률 변수(random variable) 사이의 조건부 의존성(conditional dependency)의 구조를 나타낸다.
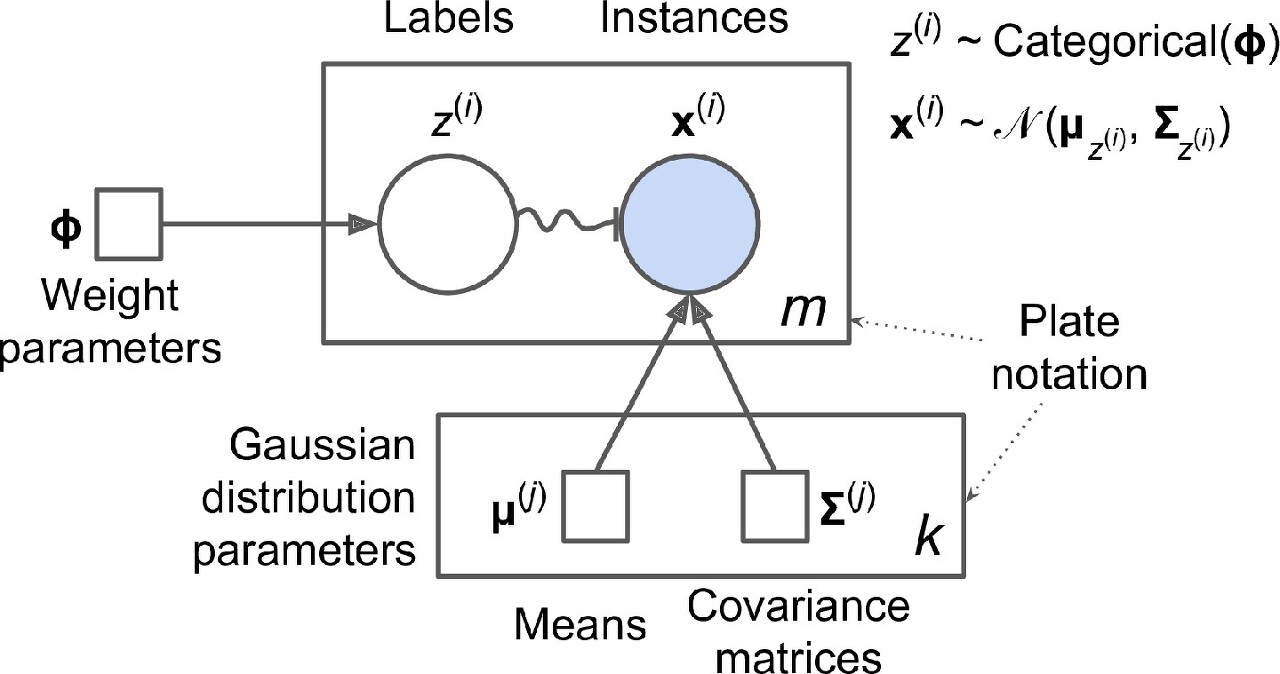
- 원은 확률 변수를 나타냄
- 사각형은 고정값을 나타냄(모델의 파라미터)
- 큰 사각형을 플레이트(plate)라고 부르며, 안의 내용이 여러 번 반복됨을 나타냄
- 각 플레이트 오른쪽 아래 숫자는 얼마나 반복되는지를 표시 -> m개의 확률 변수 z(i)(z(i)에서 z(m))와 m개의 확률 변수 x(i)가 있다. 또한 k개의 평균 μ(j)와 k개의 공분산 행렬 ∑(j)이 있다. 마지막으로 하나의 가중치 벡터 ϕ가 있다(가중치 ϕ(i)에서 ϕ(k)까지 모두 포함).
- 각 변수 z(i)는 가중치 ϕ를 갖는 범주형 분포에서 샘플링 -> 각 변수 x(i)는 해당하는 클러스터 z(i)로 정의된 평균과 공분산 행렬을 사용해 정규분포에서 샘플링
- 실선 화살표는 조건부 의존성 표현 -> 예를 들어, 각 확률 변수 z(i)의 확률 분포는 가중치 벡터 ϕ에 의존, 화살표가 플레이트 경계를 가로지르면 해당 플레이트의 모든 반복에 적용된다는 의미 -> 예를 들어, 가중치 벡터 ϕ는 확률 변수 x(1)에서 x(m)까지 모든 확률 변수의 확률 분포에 필요 조건
- z(i)에서 x(i)까지 구불구불한 화살표는 스위치(switch)를 나타냄, z(i)의 값에 따라 샘플 x(i)가 다른 가우시안 분포에서 샘플링 될 것 -> 예를 들어, z(i)=j이면 x(i)∼N(μ(j),∑(j)
- 색이 채워진 원은 알려진 값이라는 의미이며 관측 변수(observed variable)이라 불림 <-> 알려지지 않은 확률 변수 z(i)를 잠재 변수(latent variable)이라 부름
데이터셋 X가 주어지면 가중치 ϕ와 전체 분포의 파라미터 μ(1)에서 μ(k)까지와 ∑(1)에서 ∑(k)까지 추정한다.
from sklearn.mixture import GaussiasnMixture
gm = GaussiasnMixture(n_components=3, n_init=10)
gm.fit(X)print(gm.weights_)
print(gm.means_)
print(gm.covariances_)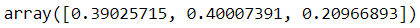

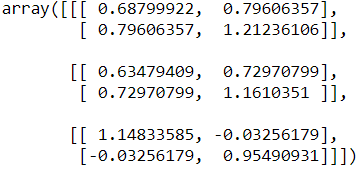
GaussianMixture 클래스는 기댓값-최대화(expectation-maximization, EM) 알고리즘을 사용한다. 이 알고리즘은 K-평균 알고리즘과 공통점이 많은데, 클러스터 파라미터를 랜덤하게 초기화하고 수렴할 때까지 두 단계를 반복한다. 먼저, 샘플을 클러스터에 할당(기댓값 단계), 그다음 클러스터를 업데이트(최대화 단계)한다.
K-평균과 달리 EM은 하드 클러스터 할당이 아니라 소프트 클러스터 할당을 사용한다. 예를 들어, 기댓값 단계에서 알고리즘은 현재 클러스터 파라미터에 기반하여 각 클러스터에 속할 확률을 예측한다. 그다음 최대화 단계에서 각 클러스터가 데이터셋에 있는 모든 샘플을 사용해 업데이트된다. 클러스터에 속할 추정 확률로 샘플에 가중치가 적용되며, 이 확률을 샘플에 대한 클러스터의 책임(responsibility)이라 부른다. 최대화 단계에서 클러스터 업데이트는 책임이 가장 많은 샘플에 크게 영향을 받는다.
EM은 K-평균처럼 나쁜 솔루션으로 수렴할 수 있다. 따라서 여러 번 실행하여(n_init = n) 가장 좋은 솔루션을 선택해야 한다.
알고리즘이 수렴했는지 여부와 반복 횟수를 확인할 수 있다.
gm.converged_ # True
gm.n_iter_ # 3이 모델은 새로운 샘플을 가장 비슷한 클러스터에 손쉽게 할당할 수 있으며(하드 군집) predict() 메서드를 사용한다. 또한 특정 클러스터에 속할 확률을 예측할 수 있는데(소프트 군집) predict_proba() 메서드를 사용한다.
gm.predict(X) # array([2, 2, 1, ... 0])
gm.predict_proba(X)GMM은 생성 모델(generative model)이며, 새로운 샘플을 만들 수 있다.
X_new, y_new = gm.sample(6)
X_new
y_new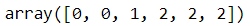
또한 주어진 위치에서 모델의 밀도를 추정할 수 있다. score_samples() 메서드를 사용하며, 샘플이 주어지면 그 위치의 확률 밀도 함수(probability density function, PDF) 로그를 예측한다. 점수가 높을수록 밀도가 높은 것이다.
gm.score_samples(X)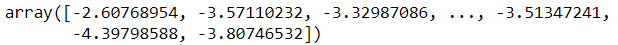
이 점수의 지숫값을 계산하면 샘플의 위치에서 PDF 값을 얻을 수 있다. 이는 하나의 확률이 아니라 확률 밀도를 가리켜서 0에서 1까지 값이 아니라 어떤 양숫값도 될 수 있다. 샘플이 특정 지역 안에 속할 확률을 예측하려면 그 지역에 대해 PDF를 적분해야 한다.
아래 그림은 모델의 클러스터 평균, 결정 경계(빨간 파선), 밀도 등고선을 보여준다.
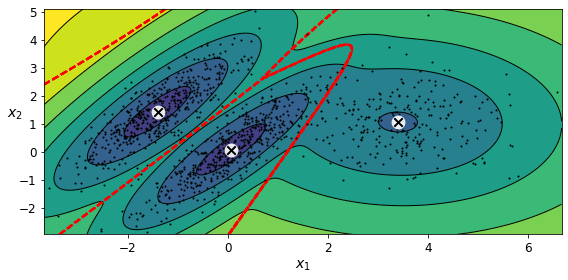
특성이나 클러스터가 많거나 샘플이 적을 때는 EM이 최적의 솔루션으로 수렴하기 어렵다. 이런 작업의 어려움을 줄이려면 알고리즘이 학습할 파라미터 개수를 제한해야 한다. 이런 방법 중 하나는 클러스터의 모양과 방향의 범위를 제한하는 것이다. 공분산 행렬에 제약을 추가하면 되는데, 사이킷런에서 covariance_type 매개변수에 다음 값 중 하나를 설정할 수 있다.
1. spherical
모든 클러스터가 원형이지만, 지름은 다를 수 있음(즉 분산이 다름)
2. diag
클러스터는 크기에 상관없이 어떤 타원형도 가능, 단 타원의 축은 좌표 축과 나란해야 함(즉 공분산 행렬이 대각 행렬이어야 함)
-> 대각 행렬은 대각선만 값이 존재하고 나머지는 0인 행렬로, 변수 간 독립 관계임을 나타냄
3. tied
모든 클러스터가 동일한 타원 모양, 크기, 방향을 가짐(즉 모든 클러스터는 동일한 공분산 행렬 공유)
covariance_type 매개변수의 디폴트는 "full"이며, 각 클러스터는 모양, 크기, 방향에 제약이 없다.
GaussianMixture 모델을 훈련하는 계산 복잡도는 샘플 개수 m, 차원 개수 n, 클러스터 개수 k와 공분산 행렬에 있는 제약에 따라 결정된다. covariance_type이 "spherical"이나 "diag"면 데이터에 어떤 클러스터 구조가 있다고 가정하므로 O(kmn)이다. covariance_type이 "tied"나 "full"이면 O(kmn2+kn3)이다. 따라서 특성 개수가 많으면 적용하기 어렵다.
9.2.1 가우시안 혼합을 사용한 이상치 탐지
GMM을 이상치 탐지에 사용하는 방법은 매우 간단한데, 밀도가 낮은 지역에 있는 모든 샘플을 이상치로 볼 수 있다. 이렇게 하려면 사용할 밀도 임곗값을 정해야 한다.
densities = gm.score_samples(X)
density_threshold = np.percentile(densities, 4) # 밀도 낮은 지역에 있는 샘플의 4% 획득
anomalies = X[densities < density_threshold]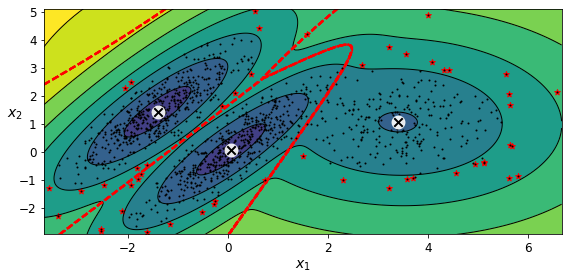
GMM은 이상치를 포함해 모든 데이터에 맞추려고 한다. 따라서 이상치가 너무 많으면 모델이 정상치를 바라보는 시각이 편향되고 일부 이상치를 정상으로 잘못 생각할 수 있다. 이를 방지하기 위해선 먼저 한 모델을 훈련하고 가장 크게 벗어난 이상치를 제거한다. 그다음 정제된 데이터셋에서 모델을 다시 훈련한다.
9.2.2 클러스터 개수 선택하기
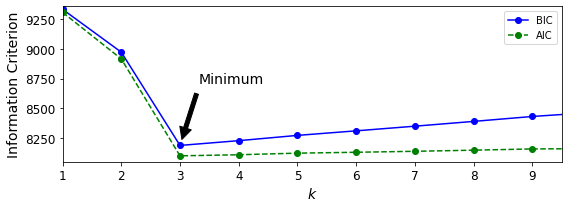
GMM에선 BIC(Bayesian information criterion)나 AIC(Akaike information criterion)와 같은 이론적 정보 기준(theoretical information criterion)을 최소화하는 모델을 찾는다.
BIC=log(m)p−2log(ˆL)
AIC=2p−2log(ˆL)
m: 샘플의 개수
p: 모델이 학습할 파라미터 개수
ˆL: 모델의 가능도 함수(likelihood function)의 최댓값
BIC와 AIC는 모두 학습할 파라미터가 많은(즉 클러스터가 많은) 모델에게 벌칙을 가하고 데이터에 잘 학습하는 모델에게 보상을 더한다.
가능도 함수란?
확률(probability)과 가능도(likelihood)는 종종 구별 없이 사용되지만, 통계학에서는 다른 의미를 가진다. 파라미터가 θ인 확률 모델이 주어지면 "확률"은 미래 출력 x가 얼마나 그럴듯한지 설명한다(파라미터 값 θ를 알고 있다면). 반면 "가능도"는 출력 x를 알고 있을 때 특정 파라미터 값 θ가 얼마나 그럴듯한지 설명한다.
PDF는 θ가 고정된 x의 함수이며, 반대로 가능도 함수는 x가 고정된 θ의 함수이다. 가능도 함수가 확률 분포가 아니라는 것을 이해해야 한다. 가능한 모든 x에 대해 확률 분포를 적분하면 항상 1이 되지만, 가능한 모든 θ에 대해 가능도 함수를 적분하면 어떤 양숫값도 될 수 있다.
데이터셋 X가 주어졌을 때 일반적으로 모델 파라미터에 대해 가장 그럴듯한 값을 예측한다. 이를 위해 X에 대한 가능도 함수를 최대화하는 값을 찾아야 한다. 이때 θ에 대한 사전 확률 분포 g가 존재한다면 L(θ|x)를 최대화하는 것보다 L(θ|x)g(θ)를 최대화하는 것이 가능하다. 이를 최대 사후 확률(maximum a-posteriori, MAP)이라고 한다. MAP가 파라미터 값을 제약하므로 이를 MLE의 규제 버전이라 생각할 수 있다.
가능도 함수를 최대화하는 것은 이 함수의 로그를 최대화하는 것과 동일하다. 예를 들어, 여러 개의 독립적인 샘플 x(1)에서 x(m)을 관측했다면 개별 가능도 함수의 곱을 최대화하는 θ를 찾아야 한다. 로그는 곱셈을 덧셈으로 바꾸기 때문에 계산하기가 훨씬 편해진다.
bic() 와 aic() 메서드를 사용하면 간단하게 구현 가능하다.
gm.bic(X)
gm.aic(X)아래 그림은 여러 가지 클러스터 개수 k에 대한 AIC와 BIC를 보여준다. k=3에서 BIC와 AIC 모두 가장 작기 때문에 최선의 선택으로 보인다.
9.2.3 베이즈 가우시안 혼합 모델
최적의 클러스터 개수를 수동으로 찾지 않고 불필요한 클러스터의 가중치를 0으로(또는 0에 가깝게) 만드는 BayesianGaussianMixture 클래스를 사용할 수 있다. 클러스터 개수 n_components 를 최적의 클러스터 개수보다 크다고 믿을 만한 값으로 지정한다(현재 문제에 대해 최소한의 정보를 가지고 있다고 가정). 이 알고리즘은 자동으로 불필요한 클러스터를 제거한다.
from sklearn.mixture import BayesianGaussianMixture
bgm = BayesianGaussianMixture(n_components=10, n_init=10) # 10으로 초기화
bgm.fit(X)
np.round(bgm.weights_, 2)
# array([0.4, 0.21, 0.4, 0., 0., ..., 0. ])위 결과를 보면 알고리즘이 자동으로 3개의 클러스터가 필요함을 감지했다. 이 모델에서 클러스터 파라미터(가중치, 평균, 공분산 행렬 등)는 더는 고정된 모델 파라미터가 아니라 클러스터 할당처럼 잠재 확률 변수로 취급된다.
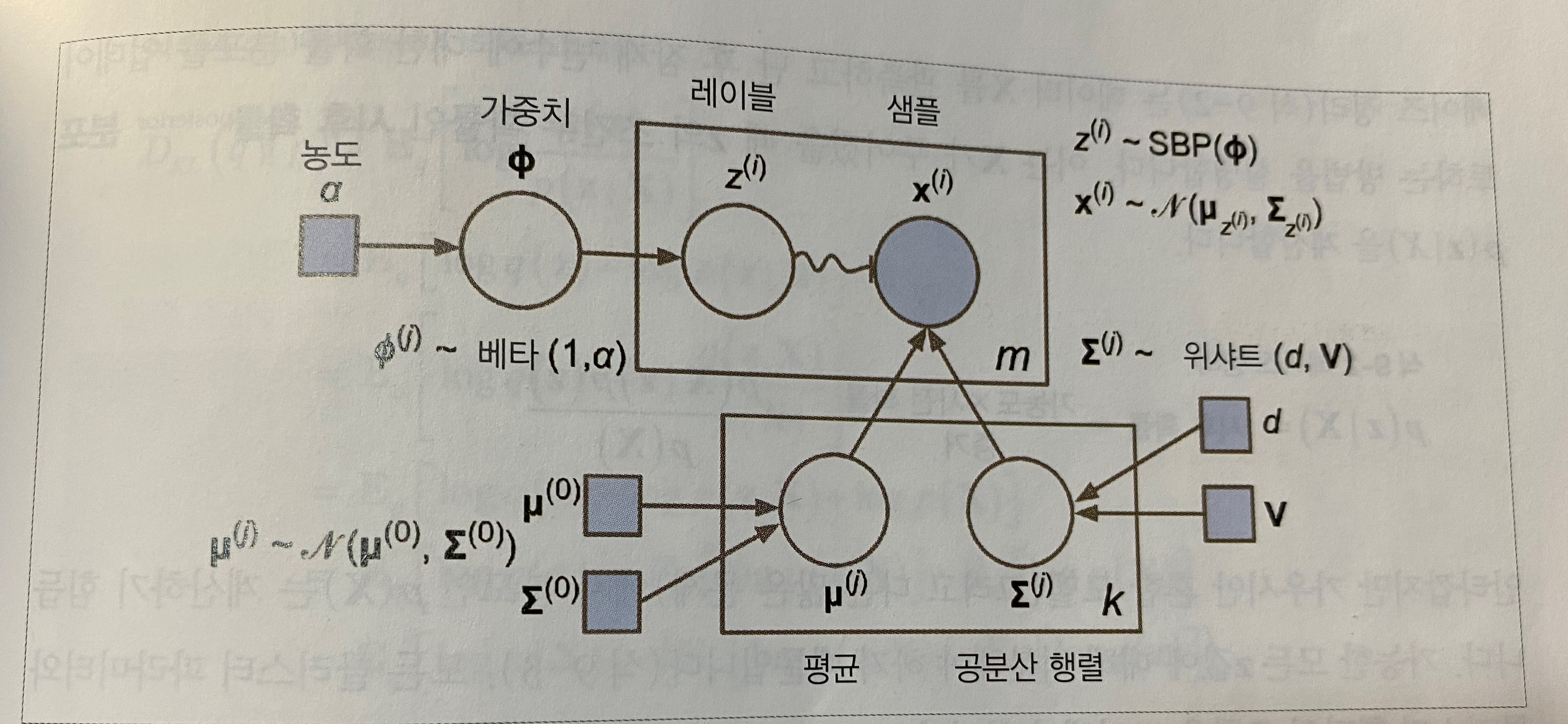
베타 분포(beta distribution)는 고정 범위 안에 놓인 값을 가진 확률 변수를 모델링할 때 자주 사용된다. SBP(stick-breaking process)를 예로 들어보자. Φ = [0.3, 0.6, 0.5]를 가정하면 샘플의 30%가 클러스터 0에 할당되고 남은 샘플의 60%가 클러스터 1에 할당된다. 그다음 남은 샘플의 50%가 클러스터 2에 할당되는 식이다.
농도(concentration) α가 크면 Φ값이 0에 가깝게 되고 SBP는 많은 클러스터를 만든다. 반대로 농도가 낮으면 Φ값이 1에 가깝데 되고 몇 개의 클러스터만 만들어 진다. 마지막으로 위샤트 분포(Wishart distribution)를 사용해 공분한 행렬을 샘플링한다. 파라미터 d와 V가 클러스터 분포 모양을 제어한다.
잠재 변수 z에 대한 사전 지식이 사전 확률(prior)이라는 확률 분포 p(z)에 인코딩될 수 있다. 예를 들어, 클러스터가 적을 것(낮은 농도)이라는 사전 믿음(prior belif)을 가질 수 있다. 반대로 풍부하다고(높은 농도) 믿을 수도 있다. 이런 클러스터 개수에 대한 사전 믿음은 weight_concentration_prior 매개변수를 사용해 조정할 수 있다.
하지만 데이터가 많을수록 사전 믿음은 중요하지 않다. 큰 차이가 나려면 사전 믿음이 매우 강하고 데이터는 적어야 한다.
베이즈 정리는 데이터 X를 관측하고 난 후 잠재 변수에 대한 확률 분포를 업데이트하는 방법을 설명한다. 이는 X가 주어졌을 때 z의 조건부 확률인 사후 확률(posterior) 분포 p(z|X)를 계산한다.
p(z|X) = 사후 확률 = 가능도 x 사전 확률 / 증거 = p(X|z)p(z)p(X)
안타깝지만 GMM에서 분모인 p(X)는 계산하기 힘들다. 가능한 모든 z값에 대해 적분해야 하기 때문이다. 모든 클러스터 파라미터와 클러스터 할당의 조합을 고려해야 하는 것이다.
p(X)=∫p(X|z)p(z)dz
이는 베이즈 통계학에 있는 주요 문제로, 몇 가지 해결 방법이 있긴 하다. 그중 하나가 변분 추론(variational inference)이다. 이 방식은 자체적인 변분 파라미터(variational parameter) λ를 가진 분포 패밀리(family of distribution) q(z;λ)를 선택한다. 그다음 q(z)가 p(z|X)의 좋은 근삿값이 되도록 이 파라미터를 최적화한다. q(z)에서 p(z|X)로의 KL 발산(Kullback-Leibler divergence, DKL(q||p)라고 씀)을 최소화하는 λ값을 찾아 이를 해결해야 한다.
위의 경우 KL 발산 공식은 아래와 같다.
DKL(q||p)=Eq[logq(z)p(z|X)]
=Eq[logp(X)]−(Eq[logp(z,X)]−Eq[logq(z)])
=logp(X)−ELBO
결국 증거의 로그(logp(x))에서 증거 하한(ELBO, evidence lower bound)을 뺀 식으로 쓸 수 있다. 증거의 로그는 q에 의존하지 않고 상수항으로 KL 발산을 최소화하려면 ELBO를 최대화해야 한다. 말이 어려운데 KL 발산은 엔트로피(entropy)와 연관되어 이해하면 된다.
정보이론에서 말하는 엔트로피는 불확실성에 대한 척도로 아래의 공식으로 계산한다.
H(q)=−∑Cc=1q(yc)log(q(yc))
이때 C는 범주 갯수이고, q는 사건의 확률질량함수(probability mass function)이다. 즉 실제 범주에 속한 갯수가 몇 개인지 알면 구할 수 있는 것이다. 반면, 크로스 엔트로피(cross entropy)는 실제 분포인 q를 모르는 상태에서 이를 예측하는 모델링을 통해 p분포를 만드는 것으로 아래와 같이 계산한다.
Hp(q)=−∑Cc=1q(yc)log(p(yc))
예측 모형을 통해 q를 예측하려 하기 때문에 크로스 엔트로피는 항상 엔트로피보다 크다.
KL 발산의 기본 정의는 서로 다른 두 분포 차이(dissimilarity)를 측정하는 데 쓰이는 척도다. 위의 엔트로피와 크로스 엔트로피를 대입하면 두 엔트로피 간의 차이로 계산된다.
DKL(q||p)=−∑Cc=1q(yc)[log(p(yc))−log(q(yc))]=Hp(q)−H(q)
크로스 엔트로피가 엔트로피보다 항상 크기 때문에 KL 발산 역시 0보다 큰 값을 갖는다. 예측 모형 분포인 p를 q에 가깝게 하는 것이 목적이므로 이 경우 KL 발산 역시 0에 가까워진다. 이때 H(q)는 고정이고, 따라서 Hp(q)를 최소화하는 것이 예측 모형을 최적화한다고 볼 수 있다. 위에서 기술한 증거 하한이 바로 이와 관련된 내용이다.2
KL 발산에 대한 시각화는 아래 공돌이의 수학정리노트 님의 글을 확인해보길 바란다.

ELBO를 최대화하는 간단한 방법은 블랙박스 확률적 변분 추론(BBSVI, blackbox stochastic variational inference)이다. 각 반복에서 몇 개의 샘플을 q에서 뽑아 변분 파라미터 λ에 대한 ELBO의 그레이디언트를 추정하는 데 사용한다. 그다음 경사 상승법 스텝에서 사용한다.
9.2.4 이상치 탐지와 특이치 탐지를 위한 다른 알고리즘
사이킷런에 있는 이상치 탐지와 특이치 탐지 전용 알고리즘을 간단히 소개한다.
PCA
- 보통 샘플의 재구성 오차와 이상치 재구성 오차 비교
Fast-MCD(minimum covariance determinant)
- 보통 샘플(정상치)이 하나의 가우시안 분포에서 생성되었다고 가정
- 해당 가우시안 분포에서 생성되지 않은 이상치로 데이터셋이 오염되었다고 가정
- 알고리즘이 가우시안 분포의 파라미터(즉 정상치를 둘러싼 타원 도형)를 추정할 때 이상치로 의심되는 샘플 무시
아이솔레이션 포레스트(isolation forest)
- 고차원 데이터셋에서 이상치 감지를 위한 효율적인 알고리즘
- 무작위로 성장한 결정 트리로 구성된 랜덤 포레스트 생성 -> 각 노드에서 특성을 랜덤하게 선택한 다음(최솟값과 최댓값 사이) 랜덤한 임곗값을 골라 데이터셋을 둘로 나눔 -> 데이터셋이 점차 분리되어 모든 샘플이 다른 샘플과 격리될 때까지 진행
- 이상치는 일반적으로 다른 샘플과 멀리 떨어져 있어 평균적으로 정상 샘플과 적은 단계에서 격리
LOF(local outlier factor)
- 주어진 샘플 주위의 밀도와 이웃 주위의 밀도 비교
- 이상치는 종종 k개의 최근접 이웃보다 더 격리됨
one-class SVM
- 기존 커널 SVM은 모든 샘플을 고차원 공간에 (암묵적으로) 매핑한 다음 선형 SVM 분류기를 사용해 두 클래스를 분리
- 여기선 샘플 클래스가 하나로 one-class SVM이 원본 공간으로부터 고차원 공간에 있는 샘플 분리
- 원본 공간에선 모든 샘플을 둘러싼 작은 영역을 찾는 것에 해당되며, 새로운 샘플이 이 영역 안에 놓이지 않으면 이는 이상치
'문돌이 존버 > 데이터 분석' 카테고리의 다른 글
| (Explainable AI) LIME 개념 이해하기 (2) | 2021.08.02 |
|---|---|
| (Explainable AI) SHAP 그래프 해석하기! feat. 실전 코드 (0) | 2021.07.30 |
| (Explainable AI) SHAP에 대해 알아보자! (2) | 2021.07.23 |
| (Explainable AI) Shapley Value에 대해 알아보자! (4) | 2021.07.22 |
| 바다나우 어텐션(Bahdanau Attention) 간단히 이해하기 (2) | 2021.07.05 |



