Collaborative Filtering 을 사용해야 하는데 기본 개념이 또 헷갈려서 아예 정리를 하기로 결정했습니다. 제가 참고한 내용은 Andrew Ng이 설명하는 Machine Learning 강의이며, 해당 강의는 코세라에서도 무료로 수강할 수 있고, 접근성이 편한 유튜브에도 업로드되어 있습니다.
Lecture 16.4 — Recommender Systems | Collaborative Filtering Algorithm — [ Andrew Ng ] - YouTube
x1는 어떤 영화가 얼마나 로맨틱한지, x2는 어떤 영화가 얼마나 액션적인지를 나타내는 특성 벡터입니다. 쉽게 말해, x1의 첫 번째 벡터는 "Love at last"라는 영화가 얼마나 로맨틱한지를 숫자로 나타낸 것이죠. x2 첫 번째 벡터는 해당 영화가 얼마나 액션적인지를 나타낸 것이겠구요.

아래 θ(i)는 각 유저의 취향을 나타내는 가중치 벡터인데요. 첫 번째 행은 bias이며, 여기선 0이라 간주하고 넘어가겠습니다. 두 번째 행은 로맨틱한 영화를 좋아하는지, 세 번째 행은 액션 영화를 좋아하는지를 나타내고 있습니다. Alice와 Bob은 로맨틱한 영화를 좋아하는 반면, Carol과 Dave는 액션적인 영화를 좋아하네요.

우리는 x1, x2 특성 벡터 값을 알고 싶습니다. 이를 어떻게 추정(approximation)할 수 있을까요? 바로 사용자가 특정 영화를 보고 남긴 평점을 바탕으로 추정합니다. "Love at last"를 예로 들면, Alice와 Bob이 5점을 준 것으로 보아 아마도 로맨틱한 영화가 아닐까 생각해볼 수 있겠죠. 반면, Carol과 Dave는 0점을 줬기 때문에 액션 영화는 아닐 것입니다. 이를 토대로 생각한다면 x1의 첫 번째 벡터는 1.0, x2의 첫 번째 벡터는 0.0이 되겠죠.
이를 간단한 수식으로 나타내면 아래와 같습니다. 실제 사용자가 매긴 평점에 가까워지도록 영화 특성 벡터를 잘 찾아야 합니다.
(θ(1))Tx(1)≈ 5
(θ(2))Tx(1)≈ 5
(θ(3))Tx(1)≈ 0
(θ(4))Tx(1)≈ 0
우리가 예상하는 영화 특성 벡터는 다음과 같습니다.
x(1)=[11.00.0]
이제 전체 특성 벡터를 구하기 위한 최적화 알고리즘의 식은 아래와 같습니다. θ(1),θ(2)...가 주어졌을 때, x(i)를 학습하는 과정입니다.
i: movie i
j: user j
n: # of movies
r(i, j): 1 if user j has rated movie i
y(i, j): rating given by user j to movie i(defined only if r(i, j) = 1)
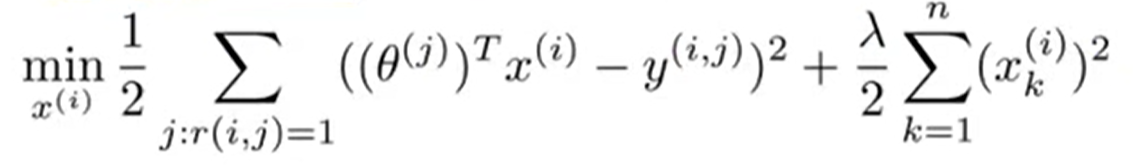
모든 영화 특성에 대한 벡터를 구하려면 아래와 같이 nm까지 다 더해주면 되겠죠?
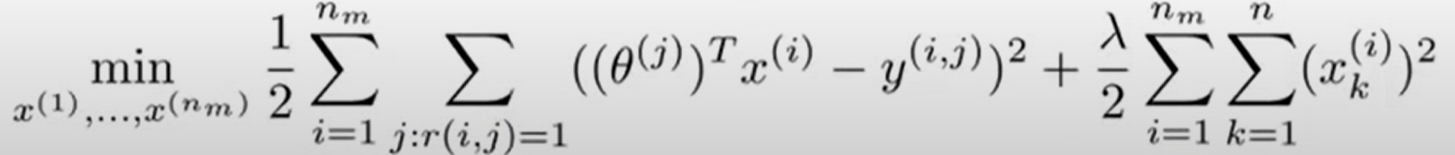
정리하자면 우리는 사용자의 취향을 담고 있는 벡터 θ(1),...,θ(n)가 주어졌을 때, 특정 영화가 로맨틱한지, 액션적인지 등 특성 벡터 x(1),...,x(m)를 추정하고자 하는 것입니다.
그렇다면 어떻게 사용자 취향 벡터가 먼저 주어졌느냐 하는 궁금증이 생기실 수도 있습니다. 이는 Collaborative Filtering이 아닌 Content-based Filtering 기법으로 구하는 것입니다. 간단히 설명하자면, 영화의 콘텐츠가 무엇이냐, 즉 로맨틱하냐, 액션적이냐, 코미딕하냐 등의 특성 벡터를 바탕으로 사용자 취향 벡터를 추정하는 것입니다.
이는 치킨 게임과도 같은데요, 무엇을 먼저 랜덤 초기화해서 구하느냐에 따라 사용자 취향 벡터를 추정할 수도, 영화 특성 벡터를 추정할 수도 있는 것입니다. 앤드류 응은 이 2개의 과정을 반복하면 Collaborative Filtering 알고리즘이 수렴하기 때문에 더 나은 추정을 할 수 있다고 합니다. 하지만 단순 반복 대신 아래와 같이 동시에 사용자 취향 벡터와 영화 특성 벡터를 추정하는 것이 더 효과적이라고 합니다. 최적화 함수를 통해 구하려는 파라미터가 2가지(파란색 밑줄)가 되는 것이죠.
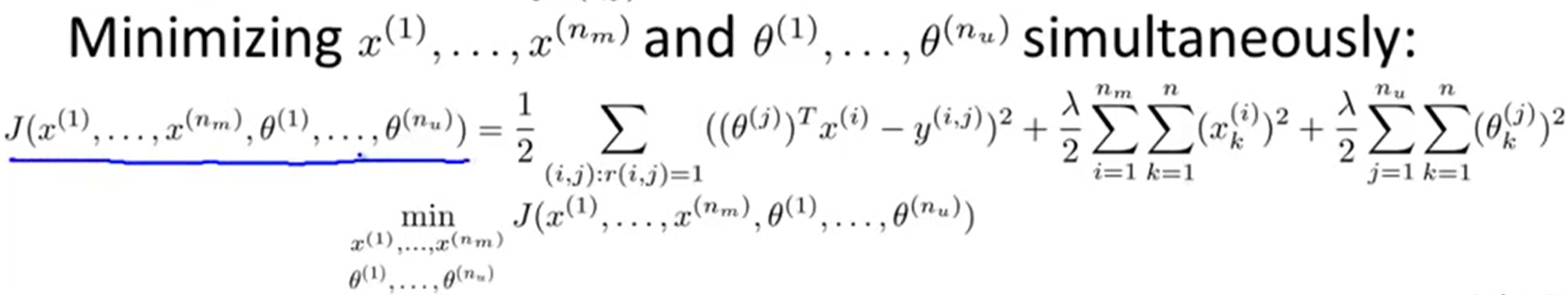
사실 어렵지 않은 식입니다. 위에서 설명한 영화 특성 벡터 추정식에다가 Content-based Filtering 기법을 통해 구한 사용자 취향 벡터 추정식을 더하기만 하면 되거든요. 사용자 취향 벡터 추정식은 아래와 같습니다. 위의 식과 다른 점은 빨간색 밑줄로 표시한 부분밖에 없습니다. 즉 사용자 취향 벡터를 알고 싶기 때문에 사용자가 대상이 되는 것이죠.(위의 식은 영화 특성이 대상이 되었죠.)
Loss 값을 구하는, 쉽게 말해 예측값과 실제값 간의 차이를 구하는 식(초록색 박스)은 똑같습니다. 사용자 취향과 영화 특성 벡터를 구하고 서로 곱해주면(inner product) 추정한 사용자 평점 행렬이 나올 것입니다. 이를 실제 사용자 평점 행렬과 비교하는 것이죠.
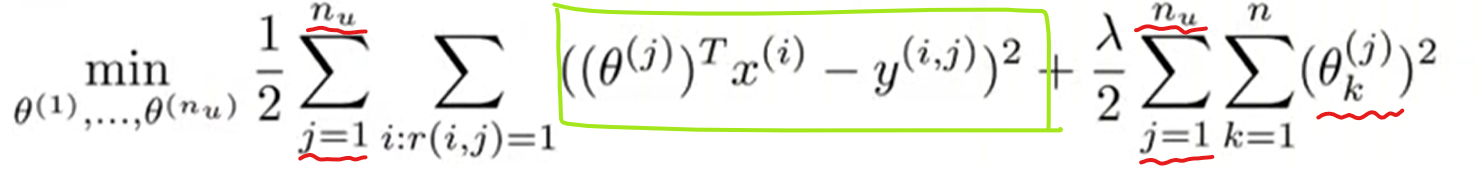
추가로 이야기드릴 것은 절편(intercept term)에 관한 것인데요. 사용자 취향 벡터든, 영화 특성 벡터든 절편이 존재하는데 앤드류 응에 따르면 이를 굳이 포함시키지 않아도 된다고 합니다. 이미 다른 가중치들이 있어 하드 코딩(hard-code)할 필요가 없으며 항상 1인 값이라 유용한 정보를 제공하지 않는다는 것이죠. 따라서 θ든, x든 모두 n+1 차원이 아닌 n차원이 됩니다.
최종 Collaborative Filtering 알고리즘은 한 마디로 사용자 취향 벡터와 영화 특성 벡터 모두 매우 작은 값으로 초기화하고 이후 경사하강법이든, 다른 최적화 알고리즘을 사용하여 최적의 파라미터 값을 찾아가는 것입니다. 최적의 파라미터란 물론 Loss 값을 최소화하는 값이겠죠. 그리고 이 두 벡터를 통해 사용자가 아직 보지 않은, 혹은 봤는데 평점을 매기지 않은 영화에 몇 점을 매길지 예상하면 됩니다.
앤드류 응 강의에선 이를 설명하는 별도의 용어가 언급되진 않았지만, 사용자 취향 벡터와 영화 특성 벡터를 구하는 과정을 Matrix Factorization이라고 부릅니다. 이 2개의 벡터를 잠재 벡터(Latent vector)라고 표현하는데, 눈에 보이는 영화 평점 데이터만을 가지고 눈에 보이지 않는 (숨겨진) 취향 및 특성 벡터를 찾기 때문입니다.
참고로 Matrix Factorization에 사용되는 알고리즘에는 PCA, NMF, SVD 등이 있는데, 가장 유명한 알고리즘으로는 SVD를 들 수 있습니다. SVD를 사용한 Collaborative Filtering 예제는 다음 시간에 살펴보겠습니다.
사용자-아이템 기반 협업 필터링(Collaborative Filtering) feat. Matrix Factorization
협업 필터링은 1) Model based, 2) Memory based로 나뉘게 됩니다. Memory based 알고리즘은 사용자-아이템 행렬을 생성하여 유사도를 측정하는 것입니다. 사용자 간 유사도를 측정하면 사용자 기반(User-based)
moondol-ai.tistory.com
'문돌이 존버 > 코딩연습' 카테고리의 다른 글
| AI가 예측하는 미스트롯2 진선미는 누구? (0) | 2021.03.03 |
|---|---|
| 파이토치(pytorch) 텐서 기본 개념 이해하기, feat. Colab (0) | 2021.01.04 |
| git 기본 지식 쌓기(2) (0) | 2020.09.17 |
| 파이썬 웹크롤링(web-crwaling) 파헤치기! feat. BeautifulSoup, Selenium (0) | 2020.07.18 |
| git 기본 지식 쌓기(1) (0) | 2020.07.11 |



