핸즈온 머신러닝 2 복습하기(챕터 17: 오토인코더와 GAN을 사용한 표현 학습과 생성적 학습)
오토인코더(autoencoder)는 어떤 지도 없이도(레이블이 없는 훈련 데이터 사용) 잠재 표현(latent representation) 및 코딩(coding)이라 부르는 입력 데이터의 밀집 표현을 학습할 수 있는 인공 신경망이다. 강력한 특성 추출기처럼 작동하므로 심층 신경망의 비지도 사전훈련에 사용될 수 있고, 생성 모델(generative model)처럼 훈련 데이터와 매우 비슷한 새로운 데이터를 생성할 수도 있다.
오토인코더와 생성적 적대 신경망(GAN: generative adversarial networks)은 모두 비지도 학습이며, 둘 다 밀집 표현을 학습하고 생성 모델로 사용할 수 있다. 비슷한 애플리케이션이 많지만 작동 방식은 크게 다르다.
- 오토인코더는 단순히 입력을 출력으로 복사하는 방법을 배운다. 이때 다양한 방법으로 네트워크에 제약을 가해 해당 작업을 오히려 어렵게 만든다. 예를 들어 잠재 표현의 크기를 제한하거나 입력에 잡음을 추가하고 원본 입력을 복원하도록 네트워크를 훈련할 수 있다. 이런 제약은 오토인코더가 단순히 입력을 출력으로 바로 복사하지 못하도록 막고 데이터를 효율적으로 표현하는 방법을 배우게 만든다.
- GAN은 신경망 2개로 구성된다. 생성자(generator)는 훈련 데이터와 비슷하게 보이는 데이터를 생성하고, 판별자(discriminator)는 가짜 데이터와 진짜 데이터를 구별한다. 이 구조는 신경망이 훈련하는 동안 생성자와 판별자가 서로 경쟁한다는 것이 핵심이다.
17.1 효율적인 데이터 표현
오코인코더는 항상 두 부분으로 구성된다. 입력을 내부 표현으로 바꾸는 인코더(=인지 네트워크)와 내부 표현을 출력으로 바꾸는 디코더(=생성 네트워크)이다.

오토인코더가 입력을 재구성하기 때문에 출력을 종종 재구성(recontruction)이라 부르고, 비용 함수는 재구성이 입력과 다를 때 모델에 벌점을 부과하는 재구성 손실(recontruction loss)을 포함한다.
내부의 표현이 입력 데이터보다 저차원이기 때문에 이런 오토인코더를 과소완전(undercomplete)이라고 한다. 과소완전 오토인코더는 입력을 코딩으로 간단히 복사할 수 없으며, 입력과 똑같은 것을 출력하기 위한 다른 방법을 찾아야 한다. 이는 입력 데이터에서 가장 중요한 특성을 학습하도록 만든다.
17.2 과소완전 선형 오토인코더로 PCA 수행하기
오토인코더가 선형 활성화 함수만 사용하고 비용 함수가 MSE라면, 이는 결국 PCA를 수행하는 것으로 볼 수 있다. 다음 코드는 3D 데이터셋에 PCA를 적용해 2D에 투영하는 간단한 선형 오토인코더를 만든다.
from tensorflow import keras
encoder = keras.models.Sequential([keras.layers.Dense(2, input_shape=[3])])
decoder = keras.models.Sequential([keras.layers.Dense(3, input_shape=[2])])
autoencoder = keras.models.Sequential([encoder, decoder])
autoencoder.compile(loss='mse', optimizer=keras.optimizers.SGD(lr=0.1))- 오토인코더를 인코더와 디코더 2개 컴포넌트로 구성한다. 둘 다 하나의 Dense 층을 가진 일반적인 Sequential 모델이다. 오토인코더는 인코더 다음에 디코더가 뒤따르는 Sequential 모델이다.
- 오토인코더의 출력 개수가 입력 개수와 동일하다.
이 모델을 훈련할 땐 다음과 같다.
history = autoencoder.fit(X_train, X_train, epochs=20)
codings = encoder.predict(X_train)동일한 데이터셋 X_train이 입력과 타깃에도 사용된다는 것에 주목하자. 아래 그림은 원본 3D 데이터셋(왼쪽)과 오토인코더의 은닉층 출력(오른쪽)을 보여준다. 오토인코더는 (PCA처럼) 데이터에 있는 분산이 가능한 많이 보존되도록 데이터를 투영할 최상의 2D 평면을 찾는다.

17.3 적층 오토인코더
은닉층을 여러 개 가진 오토인코더를 적층 오토인코더(stacked autoencoder)라고 한다. 적층 오토인코더의 구조는 전형적으로 가운데 은닉층을 기준으로 대칭이다.
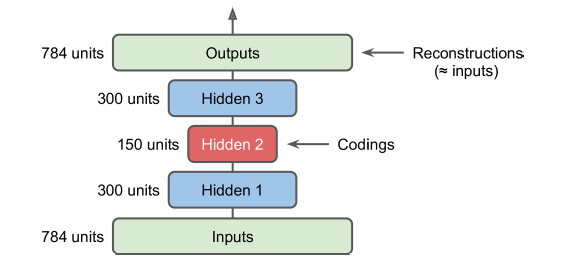
17.3.1 케라스를 사용하여 적층 오토인코더 구현하기
다음 코드는 패션 MNIST 데이터셋에서 SELU 활성화 함수를 사용해 적층 오토인코더를 만든다.
stacked_encoder = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(100, activation='selu'),
keras.layers.Dense(30, activation='selu'),
])
stacked_decoder = keras.models.Sequential([
keras.layers.Dense(100, activation='selu', input_shape=[30]),
keras.layers.Dense(28 * 28, activation='sigmoid'),
keras.layers.Reshape([28, 28])
])
stacked_ae = keras.models.Sequential([stacked_encoder, stacked_decoder])
stacked_ae.compile(loss='binary_crossentropy', optimizer=keras.optimizers.SGD(lr=1.5))
history = stacked_ae.fit(X_train, X_train, epochs=10,
validation_data=(X_valid, X_valid))17.3.2 재구성 시각화
오토인코더가 적절히 훈련되었는지 확인하는 한 가지 방법은 입력과 출력을 비교하는 것이다. 즉, 입력과 출력의 차이가 너무 크지 않아야 한다.
def plot_image(image):
plt.imshow(image, cmap='binary')
plt.axis('off')
def show_reconstructions(model, n_images=5):
reconstructions = model.predict(X_valid[:n_images])
fig = plt.figure(figsize=(n_images * 1.5, 3))
for image_index in range(n_images):
plt.subplot(2, n_images, 1 + image_index)
plot_image(X_valid[image_index])
plt.subplot(2, n_images, 1 + n_images + image_index)
plot_image(reconstructions[image_index])
show_reconstructions(stacked_ae)
17.3.3 패션 MNIST 데이터셋 시각화
오토인코더의 장점은 샘플과 특성이 많은 대용량 데이터셋을 다룰 수 있다는 점이다. 따라서 오토인코더를 사용해 적절한 수준으로 차원을 축소한 후 다른 차원 축소 알고리즘을 사용해 시각화하는 것도 전략이다. 이 방식으로 패션 MNIST 데이터셋을 시각화해본다.
먼저 적층 오토인코더의 인코더 모델을 사용해 차원을 30으로 줄인 후 t-SNE 알고리즘을 구현한 사이킷런 클래스로 시각화를 위해 차원을 2까지 줄인다.
from sklearn.manifold import TSNE
X_valid_compressed = stacked_encoder.predict(X_valid)
tsne = TSNE()
X_valid_2D = tsne.fit_transform(X_valid_compressed)plt.scatter(X_valid_2D[:, 0], X_valid_2D[:, 1], c=y_valid, s=10, cmap='tab10')
17.3.4 적층 오토인코더를 사용한 비지도 사전훈련
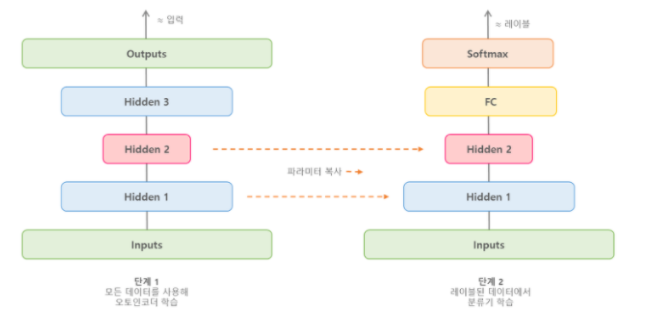
레이블된 훈련 데이터가 많지 않은 복잡한 지도 학습 문제를 다뤄야 한다면, 비슷한 문제를 학습한 신경망을 찾아 하위층을 재사용하는 것도 한 방법이다. 이렇게 하면 저수준의 특성을 학습할 필요가 없어 적은 훈련 데이터를 사용해 고성능 모델을 훈련할 수 있다. 즉, 기존의 네트워크에서 학습한 특성 감지 기능을 재사용하는 것이다.
비슷하게 대부분 레이블되지 않은 대량의 데이터셋이 있다면 먼저 전체 데이터를 사용해 적층 오토인코더를 훈련한다.
17.3.5 가중치 묶기
오토인코더가 완벽하게 대칭일 땐 디코더의 가중치와 인코더의 가중치를 묶는 것이 일반적인 방법이다. 모델에 있는 가중치 수를 절반으로 줄여서 훈련 속도를 높이고 과대적합의 위험을 줄여준다. 구체적인 예로 N개 층을 갖고 $W_L$이 $L$번째 층의 가중치를 나타낸다고 했을 때(1은 첫 번째 은닉층, N/2은 코딩 층, N은 출력층) 디코더 층의 가중치는 $W_{N-L+1}=W_L^T$와 같이 간단하게 정의할 수 있다.
다음은 케라스 사용자 정의 층을 만들어 층 간에 가중치를 묶어본다.
class DenseTranspose(keras.layers.Layer):
def __init__(self, dense, activation=None, **kwargs):
self.dense = dense
self.activation = keras.activations.get(activation)
super().__init__(**kwargs)
def build(self, batch_input_shape):
self.biases = self.add_weight(name='bias', initializer='zeros',
shape=[self.dense.input_shape[-1]])
super().build(batch_input_shape)
def call(self, inputs):
z = tf.matmul(inputs, self.dense.weights[0], transpose_b=True)
return self.activation(z + self.biases)이 사용자 정의 층은 일반적인 Dense 층과 비슷하지만 다른 Dense 층의 전치된 가중치를 사용한다(디코더에선 인코더와 달리 복원하는 역할이기 때문). 그다음 이전과 비슷하게 새로운 적층 오토인코더를 만들고, 이 디코더의 Dense 층은 인코더의 Dense 층과 묶여 있다.
dense_1 = keras.layers.Dense(100, activation='selu')
dense_2 = keras.layers.Dense(30, activation='selu')
tied_encoder = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
dense_1,
dense_2
])
tied_decoder = keras.models.Sequential([
DenseTranspose(dense_2, activation='selu'),
DenseTranspose(dense_1, activation='sigmoid'),
keras.layers.Reshape([28, 28])
])
tied_ae = keras.models.Sequential([tied_encoder, tied_decoder])17.3.6 한 번에 오토인코더 한 개씩 훈련하기
앞서 봤던 것처럼 한 번에 전체 오토인코더를 훈련하는 것보다 아래처럼 오토인코더 하나를 훈련하고 이를 쌓아올려 한 개의 적층 오토인코더를 만들 수 있다.
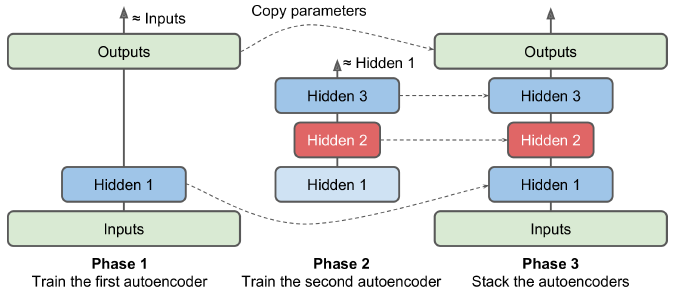
훈련 단계 1에서 첫 번째 오토인코더는 입력을 재구성하도록 학습된다. 그다음 이 오토인코더를 사용해 전체 훈련 세트를 인코딩하여 (압축된) 새 훈련 세트를 만든다(=Hidden 1). 이 새로운 훈련 세트에서 두 번째 오토인코더를 훈련한다. 마지막으로 모든 오토인코더를 사용해 전체 네트워크를 만든다.
이런 방식으로 더 많은 오토인코더를 훈련해 아주 깊은 적층 오토인코더를 만들 수 있다. 또 오토인코더는 밀집 네트워크에 국한되지 않는다. 합성곱 오토인코더나 심지어 순환 오토인코더도 만들 수 있다.
17.4 합성곱 오토인코더
이미지를 다루는 경우 오토인코더가 좋은 성능을 내지 못한다. 합성곱 신경망이 밀집 네트워크보다 훨씬 잘 맞기 때문에 (비지도 사전훈련이나 차원 축소를 위해) 이미지에 대한 오토인코더를 만드려면 합성곱 오토인코더(convolutional autoencoder)를 만들어야 한다.
인코더는 합성곱 층과 풀링 층으로 구성된 일반적인 CNN이다. 인코더는 전형적으로 입력에서 공간 방향의 차원(즉, 높이와 너비)을 줄이고 깊이(즉, 특성 맵 개수)를 늘린다. 디코더는 거꾸로 동작해야 하는데(이미지 스케일을 늘리고 깊이를 원본 차원으로 되돌리기), 이를 위해 전치 합성곱 층을 사용한다.
- 전치 합성곱 층이란, 이미지에 0으로 채워진 빈 행과 열을 삽입하여 늘린 다음 일반적인 합성곱을 수행하는 것을 의미
conv_encoder = keras.models.Sequential([
keras.layers.Reshape([28, 28, 1], input_shape=[28, 28]),
keras.layers.Conv2D(16, kernel_size=3, padding='same', activation='selu'),
keras.layers.MaxPool2D(pool_size=2),
keras.layers.Conv2D(32, kernel_size=3, padding='same', activation='selu'),
keras.layers.MaxPool2D(pool_size=2),
keras.layers.Conv2D(64, kernel_size=3, padding='same', activation='selu'),
keras.layers.MaxPool2D(pool_size=2)
])
conv_decoder = keras.models.Sequential([
keras.layers.Conv2DTranspose(32, kernel_size=3, strides=2, padding='valid',
activation='selu',
input_shape=[3, 3, 64]),
keras.layers.Conv2DTranspose(16, kernel_size=3, strides=2, padding='same',
activation='selu'),
keras.layers.Conv2DTranspose(1, kernel_size=3, strides=2, padding='same',
activation='sigmoid'),
keras.layers.Reshape([28, 28])
])
conv_ae = keras.models.Sequential([conv_encoder, conv_decoder])17.5 순환 오토인코더
시계열이나 텍스트와 같은 시퀀스에 대한 오토인코더를 만들려면 순환 신경망이 밀집 네트워크보다 더 나을 수 있다. 순환 오토인코더(recurrent autoencoder)의 경우 인코더는 일반적으로 입력 시퀀스를 하나의 벡터로 압축하는 시퀀스-투-벡터 RNN이다. 디코더는 반대로 벡터-투-시퀀스 RNN이다.
recurrent_encoder = keras.models.Sequential([
keras.layers.LSTM(100, return_sequences=True, input_shape=[None, 28]),
keras.layers.LSTM(30)
])
recurrent_decoder = keras.models.Sequential([
keras.layers.RepeatVector(28, input_shape=[30]),
keras.layers.LSTM(100, return_sequences=True),
keras.layers.TimeDistributed(keras.layers.Dense(28, activation='sigmoid'))
])
recurrent_ae = keras.models.Sequential([recurrent_encoder, recurrent_decoder])이 순환 오토인코더는 타임 스텝마다 28차원을 갖는 어떤 길이의 시퀀스로 처리할 수 있다. 타임 스텝마다 입력 벡터를 주입하기 위해 디코더의 첫 번째 층에 RepeatVector 층을 사용한 점에 주목하자.
지금까지 오토인코더가 흥미로운 특성을 학습하도록 강제하기 위해 코딩 층의 크기를 제한하여 과소완전으로 만들었다. 이외에 입력 크기만큼 또는 입력보다 큰 코딩 층을 두어 과대완전 오토인코더(overcomplete autoencoder)를 만들 수 있다.
17.6 잡음 제거 오토인코더
오토인코더가 유용한 특성을 학습하도록 강제하는 다른 방법은 입력에 잡음을 추가하고, 잡음이 없는 원본 입력을 복원하도록 훈련하는 것이다. 잡음은 입력에 추가된 순수한 가우시안(Gaussian) 잡음이거나 드롭아웃처럼 무작위로 입력을 꺼서 발생시킬 수도 있다.
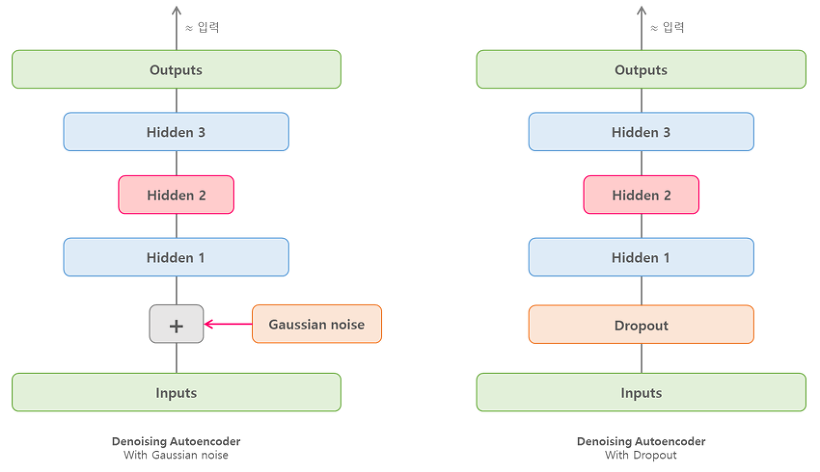
이는 인코더의 입력에 적용한 드롭아웃 층이 있는 일반적인 적층 오토인코더로, 드롭아웃 층은 훈련하는 동안에만 활성화된다.
dropout_encoder = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dropout(0.5),
keras.layers.Dense(100, activation='selu'),
keras.layers.Dense(30, activation='selu')
])
dropout_decoder = keras.models.Sequential([
keras.layers.Dense(100, activation='selu', input_shape=[30]),
keras.layers.Dense(28 * 28, activation='sigmoid'),
keras.layers.Reshape([28, 28])
])
dropout_ae = keras.models.Sequential([dropout_encoder, dropout_decoder])아래는 (픽셀 절반을 꺼서 만든) 잡음 섞인 이미지와 드롭아웃 기반의 잡음 제거 오토인코더로 재구성한 이미지다.

잡음 제거 오토인코더 역시 데이터 시각화나 비지도 사전훈련을 위해 사용할 뿐만 아니라 간단하고 효율적으로 이미지에서 잡음을 제거하는 데 사용할 수 있다.
17.7 희소 오토인코더
좋은 특성을 추출하도록 만드는 다른 제약 방식은 희소(sparsity)이다. 이는 비용 함수에 적절한 항을 추가하여 오토인코더가 코딩 층에서 활성화되는 뉴런 수를 감소시키도록 만든다. 오토인코더가 적은 수의 활성화된 뉴런을 조합하여 입력을 표현해야 하므로 각 뉴런은 유용한 특성을 표현하게 된다.
간단한 방법은 코딩 층에(코딩을 0과 1 사이 값으로 제한하기 위함) 시그모이드 활성화 함수를 사용하고 큰 코딩 층(예를 들면 300개 유닛을 가진 층)을 사용하는 것이다. 코딩 층의 활성화 값에 $l_1$ 규제를 추가한다.
sparse_l1_encoder = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(100, activation='selu'),
keras.layers.Dense(300, activation='sigmoid'),
keras.layers.ActivityRegularization(l1=1e-3)
])
sparse_l1_decoder = keras.layers.Sequential([
keras.layers.Dense(100, activation='selu', input_shape=[300]),
keras.layers.Dense(28 * 28, activation='sigmoid'),
keras.layers.Reshape([28, 28])
])
sparse_l1_ae = keras.models.Sequential([sparse_l1_encoder, sparse_l1_decoder])ActivityRegularization 층은 입력을 그대로 반환하면서 훈련 손실에 입력의 절댓값의 합을 더한다. 이 규제는 신경망이 0에 가까운 코딩을 만들도록 유도하지만 입력을 올바르게 재구성하지 못하면 벌칙을 받기 때문에 적어도 0이 아닌 값이 조금은 출력되어야 한다. $l_2$ 노름 대신 $l_1$ 노름을 사용하면 신경망이 (모든 코딩을 감소시키는 대신) 입력 이미지에서 불필요한 것을 제거하고 가장 중요한 코딩을 보전하도록 만든다.
또 다른 방법은 훈련 반복마다 코딩 층의 실제 희소 정도를 측정하고 측정된 희소 정도가 타깃 희소 정도와 다르면 모델에 벌칙을 부과하는 것이다. 이를 위해 전체 훈련 배치에 대해 코딩 층에 있는 각 뉴런의 평균적인 활성화를 계산한다.
각 뉴런에 대한 평균 활성화 정도를 알면 비용 함수에 희소 손실(sparsity loss)을 추가하여 너무 활성화되거나 충분히 활성화되지 않은 뉴런에 벌칙을 가할 수 있다. 간단한 방법은 제곱 오차(=평균 활성화 - 목표 희소 정도)를 추가하는 것이다. 하지만 실전에서 더 나은 방법은 MSE보다 훨씬 강한 그레이디언트를 가진 쿨백-라이블러 발산(Kullback-Leibler divergence)을 사용하는 것이다.
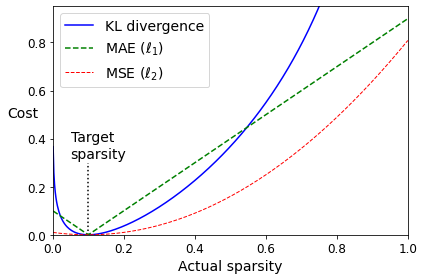
두 개의 이산 확률 분포 $P$와 $Q$가 주어졌을 때, 이 두 분산 사이의 KL 발산 $D_{KL}(P||Q)$는 아래처럼 계산한다.
$D_{KL}(P||Q) = \sum_{i} P(i) log{P(i) \over Q(i)}$
여기에선 코딩 층에서 뉴런이 활성화될 목표 확률 $p$와 실제 확률 $q$(즉, 훈련 배치에 대한 평균 활성화) 사이의 발산을 측정한다. 그러므로 계산은 아래처럼 간단해진다.
$D_{KL}(p||q) = p log{p \over q} + (1-p) log{{1-p} \over {1-q}}$
코딩 층의 각 뉴런에 대해 희소 손실을 계산했다면, 이 손실들을 모두 합해 비용 함수의 결과에 더한다. 희소 손실과 재구성 손실의 상대적 중요도를 제어하기 위해 희소 손실에 희소 가중치 파라미터를 곱한다. 이 가중치가 너무 크면 모델이 목표 희소에 가까워지지만 입력을 적절히 재구성하지 못해 쓸모없는 모델이 될 수 있다.
KL 발산 규제를 적용하기 위한 사용자 정의 규제를 만들어보자.
K = keras.backend
kl_divergence = keras.losses.kullback_leibler_divergence
class KLDivergenceRegularizer(keras.regularizers.Regularizer):
def __init__(self, weight, target=0.1):
self.weight = weight
self.target = target
def __call__(self, inputs):
mean_activities = K.mean(inputs, axis=0)
return self.weight * (
kl_divergence(self.target, mean_activities) +
kl_divergence(1. - self.target, 1. - mean_activities))코딩 층의 활성화에 KLDivergenceRegularizer를 적용해 희소 오토인코더를 만든다.
kld_reg = KLDivergenceRegularizer(weight=0.05, target=0.1)
sparse_kl_encoder = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(100, activation='selu'),
keras.layers.Dense(300, activation='sigmoid', activity_regularizer=kld_reg)
])
sparse_kl_decoder = keras.models.Sequential([
keras.layers.Dense(100, activation='selu', input_shape[300]),
keras.layers.Dense(28 * 28, activation='sigmoid'),
keras.layers.Reshape([28, 28])
])
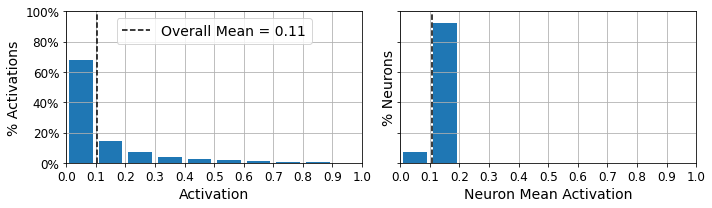
sparse_kl_ae = keras.models.Sequential([sparse_kl_encoder, sparse_kl_decoder])패션 MNIST에 희소 오토인코더를 훈련한 후 코딩 층에 있는 뉴런의 활성화가 거의 0에 가까워졌다(전체 활성화의 약 70%가 0.1보다 작음). 또한, 전체 뉴런의 평균 활성화가 0.1 근처다(전체 뉴런의 약 90%가 0.1과 0.2 사이의 평균 활성화를 가짐).
17.8 변이형 오토인코더
변이형 오토인코더는 아래의 특징들로 이전에 이야기하던 오토인코더와 매우 다르다.
- 확률적 오토인코더(probabilistic autoencoder)다. 훈련이 끝난 후에도 출력이 부분적으로 우연에 의해 결정된다.
(반면, 잡음 제거 오토인코더는 훈련 시에만 무작위성 사용)
- 생성 오토인코더(generative autoencoder)라는 것이 핵심이다. 훈련 세트에서 샘플링된 것 같은 새로운 샘플을 생성할 수 있다.
변이형 오토인코더는 효율적인 근사 베이즈 추론 방법인 변분 베이즈 추론(variational Bayesian inference)를 수행한다.
변이형 오토인코더 수행 방식은 아래와 같다.
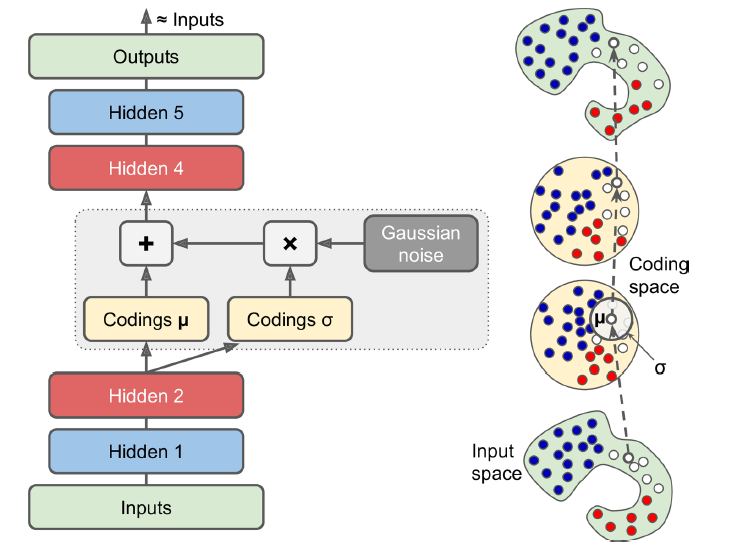
주어진 입력에 대한 코딩을 바로 만드는 대신, 인코더가 평균 코딩(mean coding) $\mu$와 표준편차 $\alpha$를 만든다. 실제 코딩은 평균이 $\mu$이고 표준편차가 $\alpha$인 가우시안 분포에서 랜덤하게 샘플링된다.
훈련하는 동안 비용 함수가 코딩을 가우시안 샘플들의 군집처럼 보이도록 코딩 공간(coding space, 또는 latent space) 안으로 점진적으로 이동시킨다.
비용 함수는 두 부분으로 구성된다. 1) 오토인코더가 입력을 재생산하도록 만드는 일반적인 재구성 손실, 2) 단순한 가우시안 분포에서 샘플된 것 같은 코딩을 가지도록 오토인코더를 강제하는 잠재 손실(latent loss)이다. 여기선 목표 분포(가우시안 분포)와 실제 코딩 분포 사이의 KL 발산을 사용한다. 코딩 층으로 전달될 수 있는 정보 양을 제한하는(오토인코더가 유용한 특성 학습 가능) 가우시안 잡음으로 인해 수식이 조금 복잡하다. 이를 간소화하면 아래와 같이 계산할 수 있다.
$L = - {1\over2} \sum_{i=1}^n 1+ log(\sigma_i^2) - \sigma_i^2 - \mu_i^2$
$L$: 잠재 손실
$n$: 코딩 차원
$\mu_i, \sigma_i$: $i$번째 코딩 원소의 평균, 표준편차
변이형 오토인코더의 구조에서 자주 등장하는 변경 사항은 인코더가 $\sigma$가 아니라 $\gamma=log(\sigma^2)$를 출력하는 것이다. 해당 방식이 수학적으로 안정적이고 훈련 속도를 높일 수 있다.
$L = - {1\over2} \sum_{i=1}^n 1+ \gamma_i - exp(\gamma_i) - \mu_i^2$
패션 MNIST 데이터셋을 이용해 변이형 오토인코더를 만들도록 한다. 먼저 $\mu$와 $\gamma$가 주어졌을 때 코딩을 샘플링하는 사용자 정의 층이 필요하다.
class Sampling(keras.layers.Layer):
def call(self, inputs):
mean, log_var = inputs
return K.random_normal(tf.shape(log_var)) * K.exp(log_var / 2) + mean위 Sampling 층은 두 입력 mean($\mu$)와 log_var($\gamma$)를 받는다. K.random_normal() 함수를 통해 평균이 0이고 표준편차가 1인 정규분포에서 ($\gamma$와 동일한 크기) 랜덤한 벡터를 샘플링한다. 그다음 $\sigma$를 만들기 위해 $exp(\gamma / 2)$를 곱하고 마지막으로 $\mu$를 더한다. 이는 평균이 $\mu$이고 표준편차가 $\gamma$인 정규분포에서 코딩 벡터를 샘플링한다.
coding_size = 10
inputs = keras.layers.Input(shape=[28, 28])
z = keras.layers.Flatten()(inputs)
z = keras.layers.Dense(150, activation='selu')(z)
z = keras.layers.Dense(100, activation='selu')(z)
codings_mean = keras.layers.Dense(codings_size)(z)
codings_log_var = keras.layers.Dense(codings_size)(z)
codings = Sampling()([codings_mean, codings_log_var])
variational_encoder = keras.Model(inputs=[inputs], outputs=[codings_mean, codings_log_var, codings])codings_mean($\mu$)와 codings_log_var($\gamma$)를 출력하는 두 Dense 층이 동일한 입력을 사용한다. 마지막 variational_encoder 모델은 출력 세 개를 만드는데, 조사 목적으로 codings_mean과 codings_log_var를 출력하고 실제 사용은 마지막 출력(codings)이다.
decoder_inputs = keras.layers.Input(shape=[codings_size])
x = keras.layers.Dense(100, activation='selu')(decoder_inputs)
x = keras.layers.Dense(150, activation='selu')(x)
x = keras.layers.Dense(28 * 28, activation='sigmoid')(x)
outputs = keras.layers.Reshape([28, 28])(x)
variational_decoder = keras.Model(inputs=[decoder_inputs], outputs=[outputs])위와 같이 디코더를 만들고 마지막으로 변이형 오토인코더 모델을 만들어본다.
_, _, codings = variational_encoder(inputs)
reconstructions = variational_decoder(codings)
variational_ae = keras.Model(inputs=[input], outputs=[reconstructions])
latent_loss = -0.5 * K.sum(
1 + codings_log_var - K.exp(codings_log_var) - K.square(codings_mean),
axis=-1)
variational_ae.add_loss(K.mean(latent_loss) / 784.)
variational_ae.compile(loss='binary_crossentropy', optimizer='rmsprop')
variational_ae.fit(X_train, X_train, epochs=50, batch_size=128,
validation_data=(X_valid, X_valid))각 샘플의 잠재 손실을 계산한 뒤 배치에 있는 모든 샘플의 평균 손실을 계산하고 재구성 손실에 비례해 적절한 크기가 되도록 784로 나눈다. 실제로 변이형 오토인코더의 재구성 손실은 픽셀마다 재구성 오차의 합이다. 하지만 케라스가 binary_crossentroyp 손실을 계산할 때 합이 아니라 784개 전체 픽셀(MNIST 데이터 기준 28 x 28)의 평균을 계산한다. 따라서 필요한 것보다 재구성 손실이 784배 작다.
17.8.1 패션 MNIST 이미지 생성하기
위 변이형 오토인코더를 통해 패션 의류처럼 보이는 이미지를 생성해보자. 가우시안 분포에서 랜덤한 코딩을 샘플링하여 디코딩하는 것이 전부다.
codings = tf.random.normal(shape=[12, codings_size])
images = variational_decoder(codings).numpy()17.9 생성적 적대 신경망
생성적 적대 신경망은 이안 굿펠로우(Ian Goodfellow) 등이 2014년 논문에서 제안했다. 아래와 같이 신경망 2개로 구성된다.
작성 中