트랜스포머(Transformer) 간단히 이해하기 (2)
본 글은 "딥 러닝을 이용한 자연어 처리 입문"을 학습하며 작성한 것입니다. 중간중간 제가 이해한 내용을 좀 더 풀어서 썼습니다. 문제가 된다면 비공개 처리하겠습니다.
지난 1편에 이어 계속 설명하겠습니다. 어텐션 스코어 행렬에 소프트맥스 함수를 사용하고, V 행렬을 곱하는 과정을 거치면 각 단어의 어텐션 값을 모두 가지는 어텐션 값 행렬이 나온다고 했습니다.
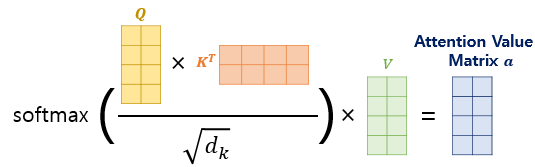
트랜스포머 논문에 기재된 수식은 아래와 같습니다.
$Attention(Q, K, V) = softmax({QK^T \over \sqrt d_k}) V$
위의 행렬 연산에 사용된 행렬의 크기를 모두 정리해봅시다. 우선 입력 문장의 길이를 $seq\_len$이라고 한다면 문장 행렬의 크기는 ($seq\_len, d_{model}$)입니다. 여기에 3개의 가중치 행렬을 곱해서 Q, K, V 행렬을 만들어야 합니다.
우선 행렬의 크기를 정의하기 위해 행렬의 각 행에 해당되는 Q벡터와 K벡터의 크기를 $d_k$라고 하고, V벡터의 크기를 $d_v$라고 해봅시다. 그렇다면 Q 행렬과 K 행렬의 크기는 ($seq\_len, d_k$)이며, V 행렬의 크기는 ($seq\_len, d_v$)가 됩니다. 그렇다면 문장 행렬과 Q, K, V 행렬의 크기로부터 가중치 행렬의 크기 추정이 가능합니다. $W^Q$와 $W^K$는 ($d_{model}, d_k$)의 크기를 가지며, $W^V$는 ($d_{model}, d_v$)의 크기를 가집니다. 다만 논문에선 $d_k$와 $d_v$의 크기는 $d_{model}/num\_heads$와 같습니다. 즉, $d_{model}/num\_heads = d_k = d_v$입니다.
결과적으로 $softmax({QK^T \over \sqrt d_k})V$ 식을 적용하여 나오는 어텐션 값 행렬 $a$의 크기는 ($seq\_len, d_v$)이 됩니다.
멀티 헤드 어텐션(Multi-head Attention)
앞서 배운 어텐션에서는 $d_{model}$의 차원을 가진 단어 벡터를 $num\_heads$로 나눈 차원을 가지는 Q, K, V벡터로 바꾸고 어텐션을 수행하였습니다. 논문 기준으로는 512의 차원의 각 단어 벡터를 8로 나누어 64차원의 Q, K, V 벡터로 바꾸어서 어텐션을 수행한 셈인데, 이제 $num\_heads$의 의미와 $d_{model}$의 차원을 가진 단어 벡터를 가지고 어텐션을 하지 않고 차원을 축소시킨 벡터로 어텐션을 수행한 이유를 알아보겠습니다.
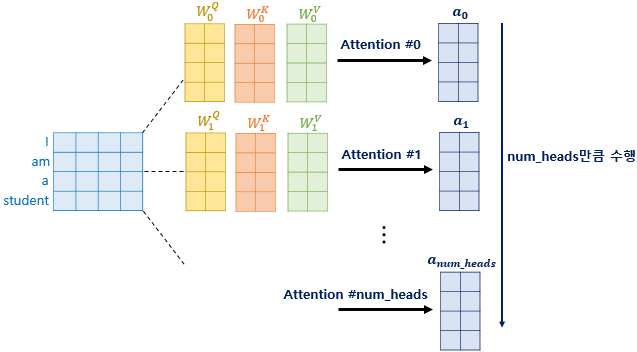
트랜스포머 연구진은 한 번의 어텐션을 하는 것보다 여러 번의 어텐션을 병렬로 사용하는 것이 더 효과적이라고 판단했습니다. 따라서 $d_{model}$의 차원을 $num\_heads$개로 나누어 $d_{model}/num\_heads$의 차원을 가지는 Q, K, V에 대해서 $num\_heads$개의 병렬 어텐션을 수행합니다. 논문에서는 하이퍼파라미터인 $num\_heads$의 값을 8로 지정했고, 8개의 병렬 어텐션이 이루어지게 됩니다. 다시 말해 위에서 설명한 어텐션이 8개로 병렬로 이루어지게 되는데, 이때 각각의 어텐션 값 행렬을 어텐션 헤드라고 부릅니다. 이때 가중치 행렬 $W^Q, W^K, W^V$의 값은 8개의 어텐션 헤드마다 전부 다릅니다.
병렬 어텐션으로 얻을 수 있는 효과는 다른 시각으로 정보들을 수집할 수 있다는 것입니다. 예를 들어보겠습니다.
앞서 사용한 예문 "그 동물은 길을 건너지 않았다. 왜냐하면 그것은 너무 피곤했기 때문이다."를 상기해봅시다. 단어 그것(it)이 Query라고 한다면, 즉 it에 대한 Q벡터로부터 다른 단어와의 연관도를 구하였을 때 첫 번째 어텐션 헤드는 '그것(it)'과 '동물(animal)'의 연관도를 높게 본다면, 두 번째 어텐션 헤드는 '그것(it)'과 '피곤했기 때문이다(tired)'의 연관도를 높게 볼 수 있습니다. 각 어텐션 헤드는 전부 다른 시각에서 보고 있기 때문입니다.

8개 어텐션 헤드의 연결 과정 이해를 위해 위의 그림에서만 $d_{model}$의 크기를 $d_v$의 8배인 16차원으로 표시
아래부터는 다시 $d_{model}$을 4차원으로 표시
병렬 어텐션을 모두 수행하였다면 모든 어텐션 헤드를 연결(concatenate)합니다. 모두 연결된 어텐션 헤드 행렬의 크기는 ($seq\_len, d_{model}$)이 됩니다.
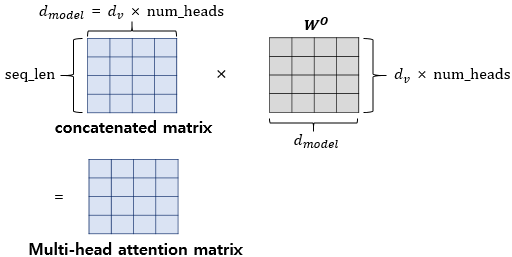
어텐션 헤드를 모두 연결한 행렬은 또 다른 가중치 행렬 $W^o$를 곱하게 되는데, 이렇게 나온 결과 행렬이 멀티-헤드 어텐션의 최종 결과물입니다. 위의 그림은 어텐션 헤드를 모두 연결한 행렬이 가중치 행렬 $W^o$와 곱해지는 과정을 보여줍니다. 이때 결과물인 멀티-헤드 어텐션 행렬은 인코더의 입력이었던 문장 행렬의 ($seq\_len, d_{model}$) 크기와 동일합니다.
인코더의 첫 번째 서브층인 멀티-헤드 어텐션 단계를 끝마쳤을 때, 인코더의 입력으로 들어왔던 행렬의 크기가 아직 유지되고 있습니다. 첫 번째 서브층인 멀티-헤드 어텐션과 두 번째 서브층인 포지션-와이즈 피드 포워드 신경망을 지나면서 인코더의 입력으로 들어온 행렬의 크기는 계속 유지되어야 합니다. 트랜스포머는 다수의 인코더를 쌓은 형태인데(논문에서는 인코더가 6개), 인코더에서의 입력의 크기가 출력에서도 동일 크기로 계속 유지되어야만 다음 인코더에서도 다시 입력이 될 수 있기 때문입니다.
패딩 마스크(Padding Mask)
입력 문장에 <PAD> 토큰이 있을 경우 어텐션에서 사실상 제외하기 위한 연산이 있습니다.
def scaled_dot_product_attention(query, key, value, mask):
... 중략 ...
logits += (mask * -1e9) # 어텐션 스코어 행렬인 logits에 mask*-1e9 값을 더해주고 있다.
... 중략 ...예를 들어 <PAD>가 포함된 입력 문장의 셀프 어텐션 예제를 봅시다. 이에 대해서 어텐션을 수행하고 어텐션 스코어 행렬을 얻는 과정은 다음과 같습니다.
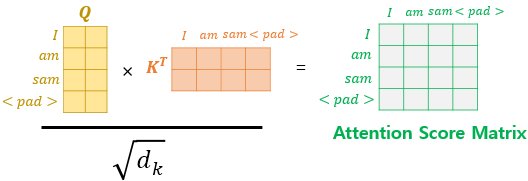
사실 단어 <PAD>의 경우에는 실질적인 의미를 가진 단어가 아닙니다. 그래서 트랜스포머에서는 Key의 경우에 <PAD> 토큰이 존재한다면 이에 대해서는 유사도를 구하지 않도록 마스킹(Masking)을 해줍니다. 마스킹이란 어텐션에서 제외하기 위해 값을 가린다는 의미입니다. 어텐션 스코어 행렬에서 행에 해당하는 문장은 Query이고, 열에 해당하는 문장은 Key입니다. 그리고 Key에 <PAD>가 있는 경우에는 해당 열 전체를 마스킹을 해줍니다.
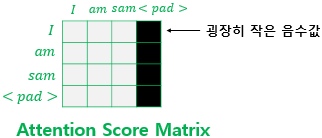
마스킹을 하는 방법은 어텐션 스코어 행렬의 마스킹 위치에 매우 작은 음수값을 넣어주는 것입니다. 여기서 매우 작은 음수값이라는 것은 -1,000,000,000처럼 $-\infty$에 가까운 수를 가리킵니다. 현재 어텐션 스코어 함수는 소프트맥스 함수를 지나지 않은 상태입니다. 앞서 배운 연산 순서라면 어텐션 스코어 함수는 소프트맥스 함수를 지나고, 그 후 Value 행렬과 곱해지게 됩니다. 그런데 현재 마스킹 위치에 매우 작은 음수 값이 들어가 있으므로 어텐션 스코어 행렬이 소프트맥스 함수를 지난 후에는 해당 위치의 값은 0에 굉장히 가까운 값이 되어 단어 간 유사도를 구하는 일에 <PAD> 토큰이 반영되지 않게 됩니다.

포지션-와이즈 피드 포워드 신경망(Position-wise FFNN)
포지션-와이즈 FFNN은 인코더와 디코더에서 공통적으로 가지고 있는 서브층입니다. 포지션-와이즈 FFNN은 쉽게 말하면 완전 연결 FFNN(Fully-connected FFNN)이라고 해석할 수 있습니다. 아래는 포지션-와이즈 FFNN의 수식을 보여줍니다.
$FFNN(x) = MAX(0, xW_1 + b_1)W_2 + b_2$
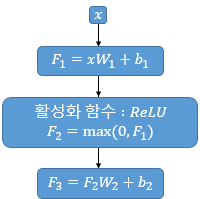
여기서 $x$는 앞서 멀티 헤드 어텐션의 결과로 나온 ($seq\_len, d_{model}$)의 크기를 가지는 행렬을 말합니다. 가중치 행렬 $W_1$은 ($d_{model}, d_{ff}$)의 크기를 가지고, 가중치 행렬 $W_2$는 ($d_{ff}, d_{model}$)의 크기를 가집니다. 논문에서 은닉층의 크기인 $d_{ff}$는 앞서 하이퍼파라미터를 정의할 때 언급했듯이 2,048의 크기를 가집니다.
여기서 매개변수 $W_1, b_1, W_2, b_2$는 하나의 인코더 층 내에서는 다른 문장, 다른 단어들마다 정확하게 동일하게 사용됩니다. 하지만 인코더 층마다는 다른 값을 가집니다.
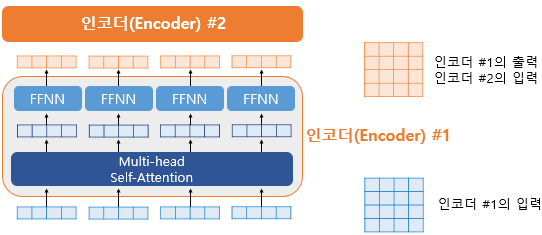
위의 그림에서 좌측은 인코더의 입력을 벡터 단위로 봤을 때, 각 벡터들이 멀티 헤드 어텐션 층이라는 인코더 내 첫 번째 서브 층을 지나 FFNN을 통과하는 것을 보여줍니다. 이는 두번째 서브층인 포지션-와이즈 FFNN을 의미합니다. 물론, 실제로는 그림의 우측과 같이 행렬로 연산되는데, 두 번째 서브층을 지난 인코더의 최종 출력은 여전히 인코더의 입력의 크기였던 ($seq\_len, d_{model}$)의 크기가 보존되고 있습니다. 하나의 인코더 층을 지난 이 행렬은 다음 인코더 층으로 전달되고, 다음 층에서도 동일한 인코더 연산이 반복됩니다.
잔차 연결(Residual connection)과 층 정규화(Layer Normalization)
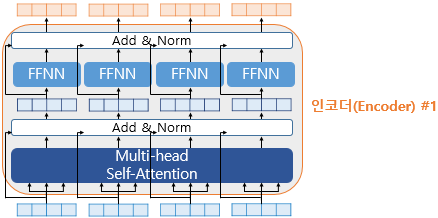
트랜스포머에서는 이러한 두 개의 서브층을 가진 인코더에 추가적으로 사용하는 기법이 있는데, 바로 Add & Norm입니다. 더 정확히는 잔차 연결과 층 정규화를 의미합니다.
위의 그림은 앞서 포지션-와이즈 FFNN을 설명할 때 사용한 그림에서 화살표와 Add & Norm(잔차 연결과 정규화 과정)을 추가한 것입니다. 추가된 화살표들은 서브층 이전의 입력에서 시작되어 서브층의 출력 부분을 향하고 있는 것에 주목합시다. 추가된 화살표가 어떤 의미를 갖고 있는지는 잔차 연결과 층 정규화를 배우고 나면 이해할 수 있습니다.
잔차 연결
잔차 연결(residual connection)의 의미를 이해하기 위해서 어떤 함수 $H(x)$에 대한 이야기를 해보겠습니다.
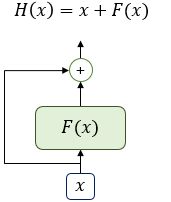
위 그림은 입력 $x$와 $x$에 대한 어떤 함수 $F(x)$의 값을 더한 함수 $H(x)$의 구조를 보여줍니다. 어떤 함수 $F(x)$가 트랜스포머에서는 서브층에 해당됩니다. 다시 말해 잔차 연결은 서브층의 입력과 출력을 더하는 것을 말합니다. 앞서 언급했듯이 트랜스포머에서 서브층의 입력과 출력은 동일한 차원을 갖고 있으므로, 서브층의 입력과 서브층의 출력은 덧셈 연산을 할 수 있습니다. 이것이 바로 위의 인코더 그림에서 각 화살표가 서브층의 입력에서 출력으로 향하도록 그려졌던 이유입니다. 잔차 연결은 컴퓨터 비전 분야에서 주로 사용되는 모델의 학습을 돕는 기법입니다.
이를 식으로 표현하면 $x + Sublayer(x)$라고 할 수 있습니다.
층 정규화
잔차 연결을 거친 결과는 이어서 층 정규화 과정을 거치게 됩니다. 잔차 연결의 입력을 $x$, 잔차 연결과 층 정규화 두 가지 연산을 모두 수행한 후의 결과 행렬을 $LN$이라고 하였을 때, 잔차 연결 후 층 정규화 연산을 수식으로 표현하자면 다음과 같습니다.
$LN = LayerNorm(x + Sublayer(x))$
층 정규화는 텐서의 마지막 차원에 대해서 평균과 분산을 구하고, 이를 가지고 특정 수식을 통해 값을 정규화하여 학습을 돕습니다. 여기서 텐서의 마지막 차원이란 것은 트랜스포머에서는 $d_{model}$차원을 의미합니다. 아래 그림은 $d_{model}$ 차원의 방향을 화살표로 표현하였습니다.
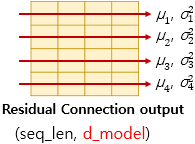
층 정규화를 위해서 화살표 방향으로 각각 평균 $\mu$과 분산 $\sigma^2$을 구합니다. 각 화살표 방향의 벡터를 $x_i$라고 해보죠.
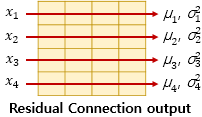
층 정규화를 수행한 후에 벡터 $x_i$는 $ln_i$라는 벡터로 정규화가 됩니다.
$ln_i = LayerNorm(x_i)$
수식을 이해하기 위해 여기서는 층 정규화를 두 가지 과정으로 나누어서 설명합니다. 1) 평균과 분산을 통한 정규화, 2) 감마와 베타를 도입하는 것입니다. 우선, 평균과 분산을 통해 벡터 $x_i$를 정규화 해줍니다. $x_i$는 벡터인 반면, 평균 $\mu_i$와 분산 $\sigma^2_i$은 스칼라입니다. 벡터 $x_i$의 각 차원을 $k$라고 했을 때, $x_{i, k}$는 다음의 수식과 같이 정규화할 수 있습니다. 다시 말해 벡터 $x_i$의 각 $k$차원의 값이 다음과 같이 정규화되는 것입니다.
$\hat{x_{i, k}} = {x_{i, k} - \mu_i \over \sqrt \sigma^2_i + \epsilon}$
$\epsilon$(엡실론)은 분모가 0이 되는 것을 방지하는 아주 작은 값입니다.
이제 $\gamma$(감마)와 $\beta$(베타)라는 벡터를 준비합니다. 초기값은 각각 1과 0입니다.
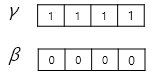
$\gamma$와 $\beta$를 도입한 층 정규화의 최종 수식은 다음과 같으며, $\gamma$와 $\beta$는 학습 가능한 파라미터입니다.
$ln_i = \gamma \hat{x_i} + \beta = LayerNorm(x_i)$
인코더에서 디코더로(From Encoder to Decoder)
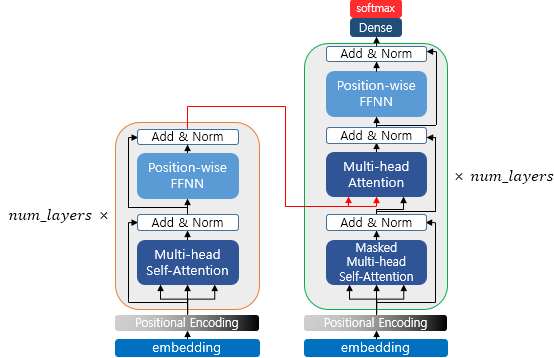
지금까지 인코더를 살펴봤습니다. 이렇게 구현된 인코더는 총 $num\_layers$만큼의 층 연산을 순차적으로 한 후에 마지막 층의 인코더의 출력을 디코더에게 전달합니다. 인코더 연산이 끝났으므로 이제 디코더 연산이 시작되어 디코더 또한 총 $num\_layers$만큼의 연산을 하는데, 이때마다 인코더가 보낸 출력을 각 디코더 층 연산에 사용합니다.
디코더의 첫 번째 서브층: 셀프 어텐션과 룩-어헤드 어텐션
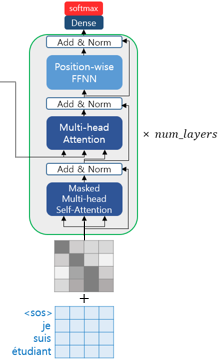
디코더 역시 인코더와 동일하게 임베딩 층과 포지셔널 인코딩을 거친 후의 문장 행렬이 입력됩니다. 트랜스포머 또한 seq2seq와 마찬가지로 교사 강요(Teacher Forcing)을 사용하여 훈련되므로 학습 과정에서 디코더는 번역할 문장에 해당되는 <sos> je suis étudiant의 문장 행렬을 한 번에 입력받습니다. 그리고 디코더는 이 문장 행렬로부터 각 시점의 단어를 예측하도록 훈련됩니다.
여기서 문제가 있습니다. seq2seq의 디코더에 사용되는 RNN 계열의 신경망은 입력 단어를 매 시점마다 순차적으로 받으므로 다음 단어 예측에 현재 시점 이전에 입력된 단어들만 참고할 수 있습니다. 반면 트랜스포머는 문장 행렬로 입력을 한 번에 받으므로 현재 시점의 단어를 예측하고자 할 때, 입력 문장 행렬로부터 미래 시점의 단어까지도 참고할 수 있는 현상이 발생합니다. 예를 들어, suis를 예측해야 하는 시점이라고 해봅시다. seq2seq의 디코더라면 현재까지 디코더에 입력된 단어는 <sos>와 je뿐일 것입니다. 하지만 트랜스포머는 이미 문장 행렬로 <sos> je suis étudiant를 입력받았습니다.
이를 위해 트랜스포머의 디코더에서는 현재 시점의 예측에서 현재 시점보다 미래에 있는 단어들을 참고하지 못하도록 룩-어헤드 마스크(look-ahead mask)를 도입했습니다. 직역하면 '미리보기에 대한 마스크'라고 할 수 있습니다.
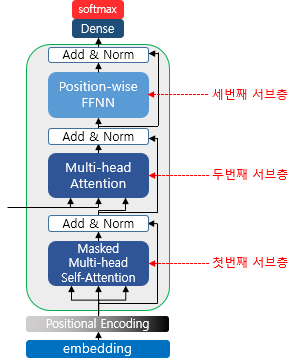
룩-어헤드 마스크는 디코더의 첫 번째 서브층에서 이루어집니다. 디코더의 첫 번째 서브층인 멀티 헤드 셀프 어텐션 층은 인코더의 첫 번째 서브층인 멀티 헤드 셀프 어텐션 층과 동일한 연산을 수행합니다. 한 가지 다른 점은 어텐션 스코어 행렬에서 마스킹을 적용한다는 점입니다. 일단 다음과 같이 셀프 어텐션을 통해 어텐션 스코어 행렬을 얻습니다.
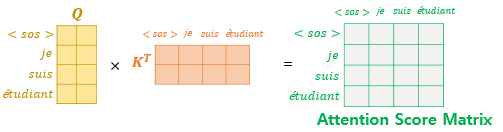
이제 자기 자신보다 미래에 있는 단어들은 참고하지 못하도록 다음과 같이 마스킹합니다.
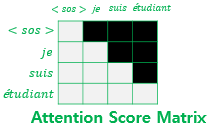
마스킹 된 후의 어텐션 스코어 행렬의 각 행을 보면 자기 자신과 그 이전 단어들만을 참고할 수 있습니다. 그 외에는 근본적으로 셀프 어텐션이라는 점과 멀티 헤드 어텐션을 수행한다는 점에서 인코더의 첫 번째 서브층과 같습니다.
룩-어헤드 마스크의 구현에 대해 알아봅시다. 룩-어헤드 마스크는 패딩 마스크와 마찬가지로 앞서 구현한 스케일드 닷 프로덕트 어텐션 함수에 mask라는 인자로 전달됩니다. 패딩 마스킹을 써야하는 경우에는 스케일드 닷 프로덕트 어텐션 함수에 패딩 마스크를 전달하고, 룩-어헤드 마스킹을 써야하는 경우에는 스케일드 닷 프로덕트 어텐션 함수에 룩-어헤드 마스크를 전달하게 됩니다.
# 스케일드 닷 프로덕트 어텐션 함수를 다시 복습해봅시다.
def scaled_dot_product_attention(query, key, value, mask):
... 중략 ...
logits += (mask * -1e9) # 어텐션 스코어 행렬인 logits에 mask*-1e9 값을 더해주고 있다.
... 중략 ...트랜스포머에는 총 세 가지 어텐션이 존재하며, 모두 멀티 헤드 어텐션을 수행하고, 멀티 헤드 어텐션 함수 내부에서 스케일드 닷 프로덕트 어텐션 함수를 호출하는데 각 어텐션 시 함수에 전달하는 마스킹은 다음과 같습니다.
1. 인코더의 셀프 어텐션 : 패딩 마스크를 전달
2. 디코더의 첫 번째 서브층인 마스크드 셀프 어텐션 : 룩-어헤드 마스크를 전달 <-- 지금 배우고 있음
3. 디코더의 두 번째 서브층인 인코더-디코더 어텐션 : 패딩 마스크를 전달
이때 룩-어헤드 마스크를 한다고해서 패딩 마스크가 불필요한 것이 아니므로 룩-어헤드 마스크는 패딩 마스크를 포함하도록 구현합니다. 룩-어헤드 마스크를 구현하는 방법은 패딩 마스크 때와 마찬가지로 마스킹을 하고자 하는 위치에는 1을, 마스킹을 하지 않는 위치에는 0을 리턴하도록 합니다.
디코더의 두 번째 서브층: 인코더-디코더 어텐션
디코더의 두 번째 서브층을 살펴봅니다. 디코더의 두 번째 서브층은 멀티 헤드 어텐션을 수행한다는 점에서는 이전의 어텐션들(인코더와 디코더의 첫 번째 서브층)과 같지만, 셀프 어텐션은 아닙니다.
셀프 어텐션은 Query, Key, Value가 같은 경우를 말하는데, 인코더-디코더 어텐션은 Query가 디코더인 행렬인 반면, Key와 Value는 인코더 행렬이기 때문입니다. 다시 한 번 각 서브층에서의 Q, K, V의 관계를 정리해봅시다.
인코더의 첫 번째 서브층: Query = Key = Value
디코더의 첫 번째 서브층: Query = Key = Value
디코더의 두 번째 서브층: Query: 디코더 행렬 / Key = Value: 인코더 행렬
디코더의 두 번째 서브층을 확대해보면 다음과 같이 인코더로부터 두 개의 화살표(빨간색)가 그려져 있습니다.
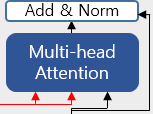
두 개의 화살표는 각각 Key와 Value를 의미하며, 이는 인코더의 마지막 층에서 온 행렬로부터 얻습니다. 반면, Query는 디코더의 첫 번째 서브층의 결과 행렬로부터 얻는다는 점이 다릅니다. Query가 디코더 행렬, Key가 인코더 행렬일 때의 어텐션 스코어 행렬을 구하는 과정은 다음과 같습니다.
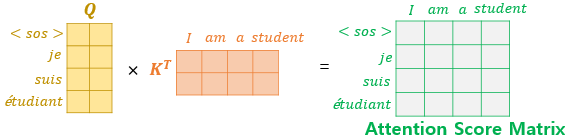
그 외에 멀티 헤드 어텐션을 수행하는 과정은 다른 어텐션들과 같습니다.
참조
딥 러닝을 이용한 자연어 처리 입문(https://wikidocs.net/31379)